class: inverse, left, bottom background-image: url(https://images.unsplash.com/photo-1601039834020-62e7a2a54e07?ixid=MXwxMjA3fDB8MHxzZWFyY2h8NDZ8fGJveGluZyUyMG9seW1waWNzfGVufDB8fDB8&ixlib=rb-1.2.1&auto=format&fit=crop&w=500&q=60) background-size: cover # .Large[theory based method and central limit theorem] ## .small[] #### .tiny[Dr. Evangeline Reynolds | Meeting 6 | 2021-02-08 | Image credit: Jonathan Thomas, Upsplash] ??? Title slide <!-- <img src="https://upload.wikimedia.org/wikipedia/commons/0/0e/Hinman_collator.jpg" width="150px"/> --> --- --- # Agenda - Housekeeping - Eye dominance Exploration Exercise #1 due next Tuesday (10 points) - project proposal due today... 4 vars...; resubmits by next Friday --- name: dolphins class: inverse background-image: url(https://images.unsplash.com/photo-1611890129309-31e797820019?ixid=MXwxMjA3fDB8MHxzZWFyY2h8OXx8ZG9scGhpbnN8ZW58MHx8MHw%3D&ixlib=rb-1.2.1&auto=format&fit=crop&w=600&q=60) background-size: cover # Could getting 15 out of 16 fish have happen just by chance? p-value - How likely is it to see as extreme or more extreme an outcome as $ \hat{p} $, if chance alone generated the outcome -- "this would only happen 1 in 1000 based on a chance model" -- $$ p - value = 1/1000 = .001 $$ --- # p-value: How often -- (the proportion of the time) -- we would see an outcome -- as extreme -- or more extreme -- than what is observed -- if the null (chance model) is true. --- # Notation ## Null Hypothesis (Chance) $$ H_0 $$ -- ## If evidence is strong against, -- then we can -- **reject the null** -- and accept the alternative hypothesis -- `$$H_A$$` --- ## Alternatively, we can use the "z score" to talk about being extreme from what would typically be observed under chance. ## How far away from the chance model center? -- ## Measure... -- ### in fish? -- ### in standard deviations; z 'standardized statisic' --- # Calculating the Z statistic $$ z = \frac{(observed - average of chance model)} / {standard deviation} $$ --- # General formula for Standard Deviation, used in simulation method: $$ SD = \sqrt\frac{\sum_{i=1}^{n}(x_i - \bar{x})^2} {n-1} $$ --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false 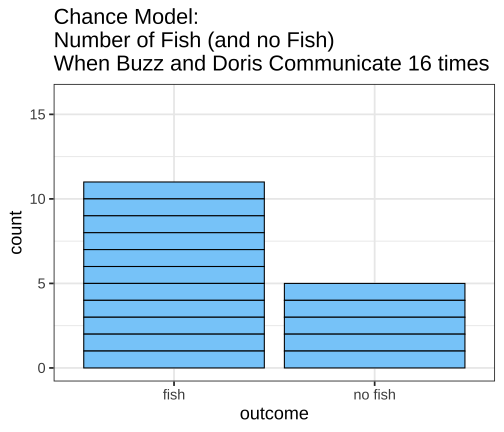<!-- --> --- count: false 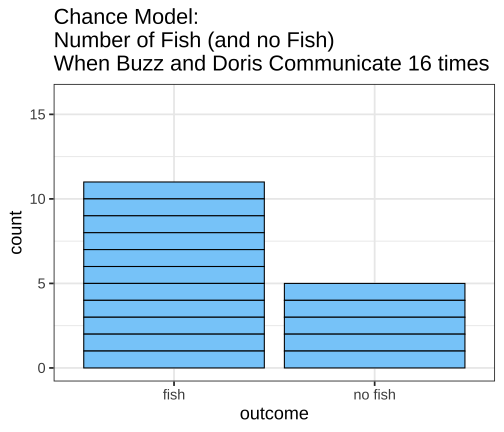<!-- --> --- count: false 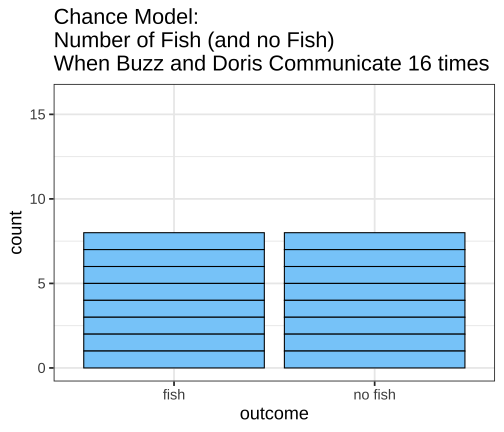<!-- --> --- count: false 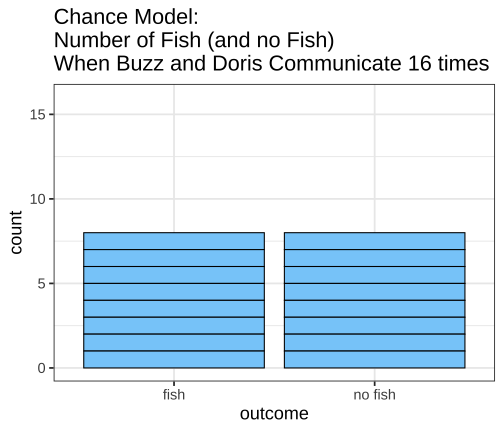<!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> <style> .panel1-dolphins_plot_chance-20 { color: black; width: 99%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel2-dolphins_plot_chance-20 { color: black; width: NA%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel3-dolphins_plot_chance-20 { color: black; width: NA%; hight: 33%; float: left; padding-left: 1%; font-size: 80% } </style> --- count: false 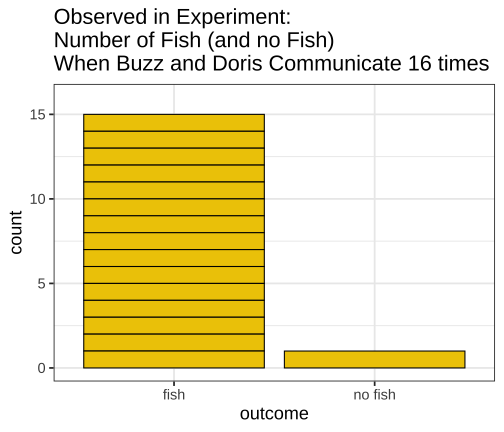<!-- --> --- count: false 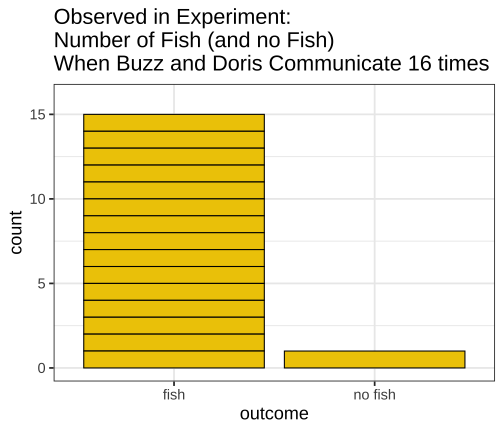<!-- --> <style> .panel1-dolphins_plot-2 { color: black; width: 99%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel2-dolphins_plot-2 { color: black; width: NA%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel3-dolphins_plot-2 { color: black; width: NA%; hight: 33%; float: left; padding-left: 1%; font-size: 80% } </style> --- count: false 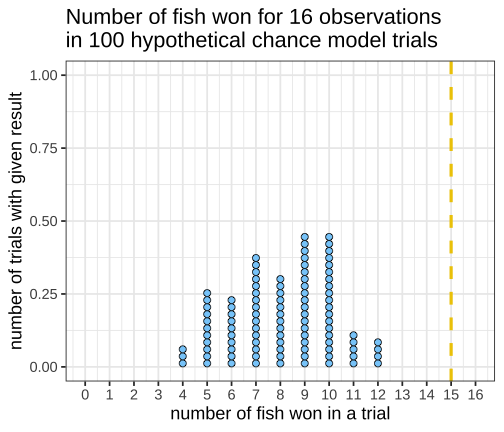<!-- --> --- count: false 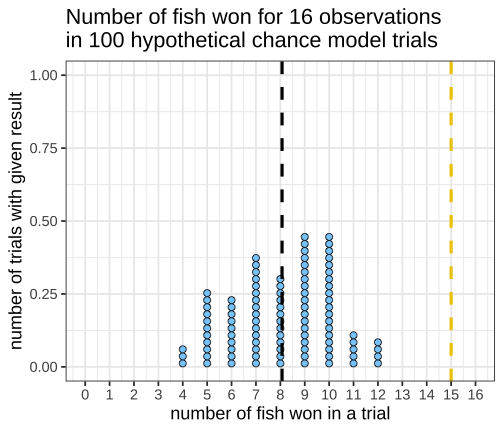<!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false <!-- --> --- count: false 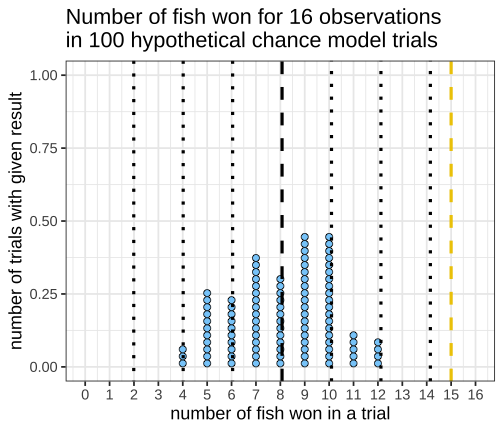<!-- --> <style> .panel1-chance_v_observed-user { color: black; width: 99%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel2-chance_v_observed-user { color: black; width: NA%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel3-chance_v_observed-user { color: black; width: NA%; hight: 33%; float: left; padding-left: 1%; font-size: 80% } </style> --- count: false 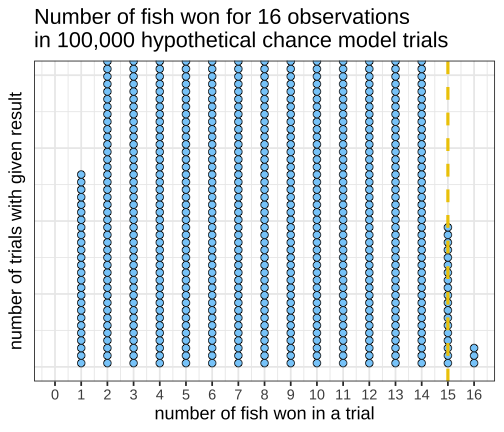<!-- --> --- count: false 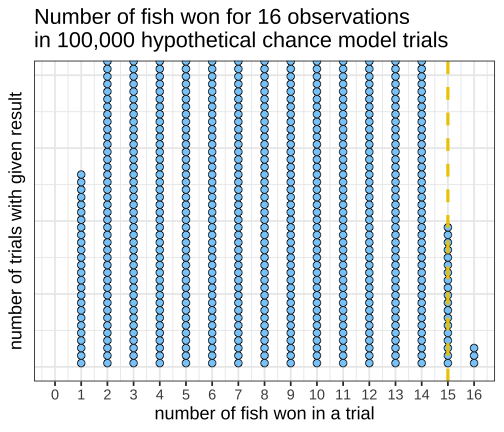<!-- --> <style> .panel1-chance_v_observed_100000-2 { color: black; width: 99%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel2-chance_v_observed_100000-2 { color: black; width: NA%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel3-chance_v_observed_100000-2 { color: black; width: NA%; hight: 33%; float: left; padding-left: 1%; font-size: 80% } </style> --- ## Consistent or not consistent w/ chance model? -- ## Z score of 1.2? -- ## Z score of 3? -- ## Z score of -1? -- ## Z score of -5? --- background-image: url(images_for_lecture/normal_histogram.svg) background-size: 550px background-position: 50% 80% #### Interpretation --- class: center, inverse, middle # Can I also calculate a p-value with the z-score? -- z-score seems imprecise. I want to know: *exactly* how unlikely to observe such extreme a case just by chance --- # Theory-based test for a single proportion -- or # 'one-proportion z-test' --- # Relies on -- the Central Limit Theorem > If the sample size (n) is large enough, sampling distributions are normally distributed... --- > --- # The Central Limit Theorem for proportions -> > The distribution of sample proportions will be bell-shaped (normal), centered at the long-run proportion (pi), with a standard deviation of: # $$ sd_{prop} = \sqrt\frac{\pi*(1-\pi)}{n} $$ --- <img src="https://thumbs.gfycat.com/QuaintTidyCockatiel-size_restricted.gif" width="80%" /> --- --- # Step 1 calculate sample proportion ## Is the proportion of Yuks is .25? ```r 13/15 ``` ``` [1] 0.8666667 ``` --- ## Step 2 calc sd for the null: ```r sqrt((.25 * (1-.25)) / 15 ) ``` ``` [1] 0.1118034 ``` --- # Step 3 calc z stat ## z stat (number of SDs away from chance model mean) ```r (0.866 - .25) / # observed minus null prop 0.1118034 ``` ``` [1] 5.509671 ``` --- # Step 4 ## situate in normal distribution ```r # pnorm gives us cumulative density function # for normal distribution 2 * (1 - pnorm(abs(5.509671))) ``` ``` [1] 3.59505e-08 ``` ```r # result is p-value # the proportion of times we expect # to see something as extreme or more extreme # than observed stat # just by chance! ``` --- count: false ## All together! .panel1-theory_p_val_calc-auto[ ```r ## calculate sample proportion p hat *13 / 15 ``` ] .panel2-theory_p_val_calc-auto[ ``` [1] 0.8666667 ``` ] --- count: false ## All together! .panel1-theory_p_val_calc-auto[ ```r ## calculate sample proportion p hat 13 / 15 -> * sample_proportion ``` ] .panel2-theory_p_val_calc-auto[ ] --- count: false ## All together! .panel1-theory_p_val_calc-auto[ ```r ## calculate sample proportion p hat 13 / 15 -> sample_proportion ## establish pi *.25 ``` ] .panel2-theory_p_val_calc-auto[ ``` [1] 0.25 ``` ] --- count: false ## All together! .panel1-theory_p_val_calc-auto[ ```r ## calculate sample proportion p hat 13 / 15 -> sample_proportion ## establish pi .25 -> * null_prob ``` ] .panel2-theory_p_val_calc-auto[ ] --- count: false ## All together! .panel1-theory_p_val_calc-auto[ ```r ## calculate sample proportion p hat 13 / 15 -> sample_proportion ## establish pi .25 -> null_prob ## calc sd for the null: *sqrt((null_prob * (1-null_prob)) / 15 ) ``` ] .panel2-theory_p_val_calc-auto[ ``` [1] 0.1118034 ``` ] --- count: false ## All together! .panel1-theory_p_val_calc-auto[ ```r ## calculate sample proportion p hat 13 / 15 -> sample_proportion ## establish pi .25 -> null_prob ## calc sd for the null: sqrt((null_prob * (1-null_prob)) / 15 ) -> * sd_chance_model ``` ] .panel2-theory_p_val_calc-auto[ ] --- count: false ## All together! .panel1-theory_p_val_calc-auto[ ```r ## calculate sample proportion p hat 13 / 15 -> sample_proportion ## establish pi .25 -> null_prob ## calc sd for the null: sqrt((null_prob * (1-null_prob)) / 15 ) -> sd_chance_model ## calculate z score *(sample_proportion - null_prob) ``` ] .panel2-theory_p_val_calc-auto[ ``` [1] 0.6166667 ``` ] --- count: false ## All together! .panel1-theory_p_val_calc-auto[ ```r ## calculate sample proportion p hat 13 / 15 -> sample_proportion ## establish pi .25 -> null_prob ## calc sd for the null: sqrt((null_prob * (1-null_prob)) / 15 ) -> sd_chance_model ## calculate z score (sample_proportion - null_prob) / * sd_chance_model ``` ] .panel2-theory_p_val_calc-auto[ ``` [1] 5.515634 ``` ] --- count: false ## All together! .panel1-theory_p_val_calc-auto[ ```r ## calculate sample proportion p hat 13 / 15 -> sample_proportion ## establish pi .25 -> null_prob ## calc sd for the null: sqrt((null_prob * (1-null_prob)) / 15 ) -> sd_chance_model ## calculate z score (sample_proportion - null_prob) / sd_chance_model -> *z_score ``` ] .panel2-theory_p_val_calc-auto[ ] --- count: false ## All together! .panel1-theory_p_val_calc-auto[ ```r ## calculate sample proportion p hat 13 / 15 -> sample_proportion ## establish pi .25 -> null_prob ## calc sd for the null: sqrt((null_prob * (1-null_prob)) / 15 ) -> sd_chance_model ## calculate z score (sample_proportion - null_prob) / sd_chance_model -> z_score # situate in normal distribution *(1 - pnorm(abs(z_score))) * 2 ``` ] .panel2-theory_p_val_calc-auto[ ``` [1] 3.475241e-08 ``` ] <style> .panel1-theory_p_val_calc-auto { color: black; width: 49%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel2-theory_p_val_calc-auto { color: black; width: 49%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel3-theory_p_val_calc-auto { color: black; width: NA%; hight: 33%; float: left; padding-left: 1%; font-size: 80% } </style> --- class: inverse, center, middle # Does this example meet the validity conditions though? -- ## No -- ## At least 10 of each case (10 'successes' 10 'failures') --- # Olympics - where theory holds (10 successes, 10 failures) --- count: false ## All together boxing! .panel1-theory_p_val_calc_box-auto[ ```r *options(scipen = 10) ``` ] .panel2-theory_p_val_calc_box-auto[ ] --- count: false ## All together boxing! .panel1-theory_p_val_calc_box-auto[ ```r options(scipen = 10) ## calculate sample proportion p hat *248 / 457 ``` ] .panel2-theory_p_val_calc_box-auto[ ``` [1] 0.5426696 ``` ] --- count: false ## All together boxing! .panel1-theory_p_val_calc_box-auto[ ```r options(scipen = 10) ## calculate sample proportion p hat 248 / 457 -> * sample_proportion ``` ] .panel2-theory_p_val_calc_box-auto[ ] --- count: false ## All together boxing! .panel1-theory_p_val_calc_box-auto[ ```r options(scipen = 10) ## calculate sample proportion p hat 248 / 457 -> sample_proportion ## establish pi *.5 ``` ] .panel2-theory_p_val_calc_box-auto[ ``` [1] 0.5 ``` ] --- count: false ## All together boxing! .panel1-theory_p_val_calc_box-auto[ ```r options(scipen = 10) ## calculate sample proportion p hat 248 / 457 -> sample_proportion ## establish pi .5 -> * null_prob ``` ] .panel2-theory_p_val_calc_box-auto[ ] --- count: false ## All together boxing! .panel1-theory_p_val_calc_box-auto[ ```r options(scipen = 10) ## calculate sample proportion p hat 248 / 457 -> sample_proportion ## establish pi .5 -> null_prob ## calc sd for the null: *sqrt((null_prob * (1-null_prob)) / 457 ) ``` ] .panel2-theory_p_val_calc_box-auto[ ``` [1] 0.02338901 ``` ] --- count: false ## All together boxing! .panel1-theory_p_val_calc_box-auto[ ```r options(scipen = 10) ## calculate sample proportion p hat 248 / 457 -> sample_proportion ## establish pi .5 -> null_prob ## calc sd for the null: sqrt((null_prob * (1-null_prob)) / 457 ) -> * sd_chance_model ``` ] .panel2-theory_p_val_calc_box-auto[ ] --- count: false ## All together boxing! .panel1-theory_p_val_calc_box-auto[ ```r options(scipen = 10) ## calculate sample proportion p hat 248 / 457 -> sample_proportion ## establish pi .5 -> null_prob ## calc sd for the null: sqrt((null_prob * (1-null_prob)) / 457 ) -> sd_chance_model ## calculate z score *(sample_proportion - null_prob) ``` ] .panel2-theory_p_val_calc_box-auto[ ``` [1] 0.04266958 ``` ] --- count: false ## All together boxing! .panel1-theory_p_val_calc_box-auto[ ```r options(scipen = 10) ## calculate sample proportion p hat 248 / 457 -> sample_proportion ## establish pi .5 -> null_prob ## calc sd for the null: sqrt((null_prob * (1-null_prob)) / 457 ) -> sd_chance_model ## calculate z score (sample_proportion - null_prob) / * sd_chance_model ``` ] .panel2-theory_p_val_calc_box-auto[ ``` [1] 1.824343 ``` ] --- count: false ## All together boxing! .panel1-theory_p_val_calc_box-auto[ ```r options(scipen = 10) ## calculate sample proportion p hat 248 / 457 -> sample_proportion ## establish pi .5 -> null_prob ## calc sd for the null: sqrt((null_prob * (1-null_prob)) / 457 ) -> sd_chance_model ## calculate z score (sample_proportion - null_prob) / sd_chance_model -> *z_score ``` ] .panel2-theory_p_val_calc_box-auto[ ] --- count: false ## All together boxing! .panel1-theory_p_val_calc_box-auto[ ```r options(scipen = 10) ## calculate sample proportion p hat 248 / 457 -> sample_proportion ## establish pi .5 -> null_prob ## calc sd for the null: sqrt((null_prob * (1-null_prob)) / 457 ) -> sd_chance_model ## calculate z score (sample_proportion - null_prob) / sd_chance_model -> z_score # situate in normal distribution *(1 - pnorm(abs(z_score))) * 2 ``` ] .panel2-theory_p_val_calc_box-auto[ ``` [1] 0.06810023 ``` ] <style> .panel1-theory_p_val_calc_box-auto { color: black; width: 49%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel2-theory_p_val_calc_box-auto { color: black; width: 49%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel3-theory_p_val_calc_box-auto { color: black; width: NA%; hight: 33%; float: left; padding-left: 1%; font-size: 80% } </style> --- ``` # A tibble: 9 × 3 some_zstats dnorm_result pnorm_result <int> <dbl> <dbl> 1 -4 0.000134 0.0000317 2 -3 0.00443 0.00135 3 -2 0.0540 0.0228 4 -1 0.242 0.159 5 0 0.399 0.5 6 1 0.242 0.841 7 2 0.0540 0.977 8 3 0.00443 0.999 9 4 0.000134 1.00 ``` --- https://evamaerey.github.io/statistics/distributions#1 --- count: false ## What's pnorm() .panel1-dnorm_pnorm-auto[ ```r *((-100:100)/20) ``` ] .panel2-dnorm_pnorm-auto[ ``` [1] -5.00 -4.95 -4.90 -4.85 -4.80 -4.75 -4.70 -4.65 -4.60 -4.55 -4.50 -4.45 [13] -4.40 -4.35 -4.30 -4.25 -4.20 -4.15 -4.10 -4.05 -4.00 -3.95 -3.90 -3.85 [25] -3.80 -3.75 -3.70 -3.65 -3.60 -3.55 -3.50 -3.45 -3.40 -3.35 -3.30 -3.25 [37] -3.20 -3.15 -3.10 -3.05 -3.00 -2.95 -2.90 -2.85 -2.80 -2.75 -2.70 -2.65 [49] -2.60 -2.55 -2.50 -2.45 -2.40 -2.35 -2.30 -2.25 -2.20 -2.15 -2.10 -2.05 [61] -2.00 -1.95 -1.90 -1.85 -1.80 -1.75 -1.70 -1.65 -1.60 -1.55 -1.50 -1.45 [73] -1.40 -1.35 -1.30 -1.25 -1.20 -1.15 -1.10 -1.05 -1.00 -0.95 -0.90 -0.85 [85] -0.80 -0.75 -0.70 -0.65 -0.60 -0.55 -0.50 -0.45 -0.40 -0.35 -0.30 -0.25 [97] -0.20 -0.15 -0.10 -0.05 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 [109] 0.40 0.45 0.50 0.55 0.60 0.65 0.70 0.75 0.80 0.85 0.90 0.95 [121] 1.00 1.05 1.10 1.15 1.20 1.25 1.30 1.35 1.40 1.45 1.50 1.55 [133] 1.60 1.65 1.70 1.75 1.80 1.85 1.90 1.95 2.00 2.05 2.10 2.15 [145] 2.20 2.25 2.30 2.35 2.40 2.45 2.50 2.55 2.60 2.65 2.70 2.75 [157] 2.80 2.85 2.90 2.95 3.00 3.05 3.10 3.15 3.20 3.25 3.30 3.35 [169] 3.40 3.45 3.50 3.55 3.60 3.65 3.70 3.75 3.80 3.85 3.90 3.95 [181] 4.00 4.05 4.10 4.15 4.20 4.25 4.30 4.35 4.40 4.45 4.50 4.55 [193] 4.60 4.65 4.70 4.75 4.80 4.85 4.90 4.95 5.00 ``` ] --- count: false ## What's pnorm() .panel1-dnorm_pnorm-auto[ ```r ((-100:100)/20) %>% * tibble(sd = .) ``` ] .panel2-dnorm_pnorm-auto[ ``` # A tibble: 201 × 1 sd <dbl> 1 -5 2 -4.95 3 -4.9 4 -4.85 5 -4.8 6 -4.75 7 -4.7 8 -4.65 9 -4.6 10 -4.55 # … with 191 more rows ``` ] --- count: false ## What's pnorm() .panel1-dnorm_pnorm-auto[ ```r ((-100:100)/20) %>% tibble(sd = .) %>% * mutate(prob_from_normal = * dnorm(sd)) ``` ] .panel2-dnorm_pnorm-auto[ ``` # A tibble: 201 × 2 sd prob_from_normal <dbl> <dbl> 1 -5 0.00000149 2 -4.95 0.00000191 3 -4.9 0.00000244 4 -4.85 0.00000311 5 -4.8 0.00000396 6 -4.75 0.00000503 7 -4.7 0.00000637 8 -4.65 0.00000805 9 -4.6 0.0000101 10 -4.55 0.0000127 # … with 191 more rows ``` ] --- count: false ## What's pnorm() .panel1-dnorm_pnorm-auto[ ```r ((-100:100)/20) %>% tibble(sd = .) %>% mutate(prob_from_normal = dnorm(sd)) %>% * mutate(cummulative_from_normal = * pnorm(sd)) ``` ] .panel2-dnorm_pnorm-auto[ ``` # A tibble: 201 × 3 sd prob_from_normal cummulative_from_normal <dbl> <dbl> <dbl> 1 -5 0.00000149 0.000000287 2 -4.95 0.00000191 0.000000371 3 -4.9 0.00000244 0.000000479 4 -4.85 0.00000311 0.000000617 5 -4.8 0.00000396 0.000000793 6 -4.75 0.00000503 0.00000102 7 -4.7 0.00000637 0.00000130 8 -4.65 0.00000805 0.00000166 9 -4.6 0.0000101 0.00000211 10 -4.55 0.0000127 0.00000268 # … with 191 more rows ``` ] --- count: false ## What's pnorm() .panel1-dnorm_pnorm-auto[ ```r ((-100:100)/20) %>% tibble(sd = .) %>% mutate(prob_from_normal = dnorm(sd)) %>% mutate(cummulative_from_normal = pnorm(sd)) %>% * ggplot() ``` ] .panel2-dnorm_pnorm-auto[ <!-- --> ] --- count: false ## What's pnorm() .panel1-dnorm_pnorm-auto[ ```r ((-100:100)/20) %>% tibble(sd = .) %>% mutate(prob_from_normal = dnorm(sd)) %>% mutate(cummulative_from_normal = pnorm(sd)) %>% ggplot() + * aes(x = sd) ``` ] .panel2-dnorm_pnorm-auto[ <!-- --> ] --- count: false ## What's pnorm() .panel1-dnorm_pnorm-auto[ ```r ((-100:100)/20) %>% tibble(sd = .) %>% mutate(prob_from_normal = dnorm(sd)) %>% mutate(cummulative_from_normal = pnorm(sd)) %>% ggplot() + aes(x = sd) + * aes(y = prob_from_normal) ``` ] .panel2-dnorm_pnorm-auto[ <!-- --> ] --- count: false ## What's pnorm() .panel1-dnorm_pnorm-auto[ ```r ((-100:100)/20) %>% tibble(sd = .) %>% mutate(prob_from_normal = dnorm(sd)) %>% mutate(cummulative_from_normal = pnorm(sd)) %>% ggplot() + aes(x = sd) + aes(y = prob_from_normal) + * labs(title = "Probability Distribution for Normal Distribution") ``` ] .panel2-dnorm_pnorm-auto[ <!-- --> ] --- count: false ## What's pnorm() .panel1-dnorm_pnorm-auto[ ```r ((-100:100)/20) %>% tibble(sd = .) %>% mutate(prob_from_normal = dnorm(sd)) %>% mutate(cummulative_from_normal = pnorm(sd)) %>% ggplot() + aes(x = sd) + aes(y = prob_from_normal) + labs(title = "Probability Distribution for Normal Distribution") + * geom_line() ``` ] .panel2-dnorm_pnorm-auto[ <!-- --> ] --- count: false ## What's pnorm() .panel1-dnorm_pnorm-auto[ ```r ((-100:100)/20) %>% tibble(sd = .) %>% mutate(prob_from_normal = dnorm(sd)) %>% mutate(cummulative_from_normal = pnorm(sd)) %>% ggplot() + aes(x = sd) + aes(y = prob_from_normal) + labs(title = "Probability Distribution for Normal Distribution") + geom_line() + * aes(y = cummulative_from_normal) ``` ] .panel2-dnorm_pnorm-auto[ <!-- --> ] --- count: false ## What's pnorm() .panel1-dnorm_pnorm-auto[ ```r ((-100:100)/20) %>% tibble(sd = .) %>% mutate(prob_from_normal = dnorm(sd)) %>% mutate(cummulative_from_normal = pnorm(sd)) %>% ggplot() + aes(x = sd) + aes(y = prob_from_normal) + labs(title = "Probability Distribution for Normal Distribution") + geom_line() + aes(y = cummulative_from_normal) + * labs(title = "Cumulative Distribution Function (CDF) for Normal Distribution") ``` ] .panel2-dnorm_pnorm-auto[ 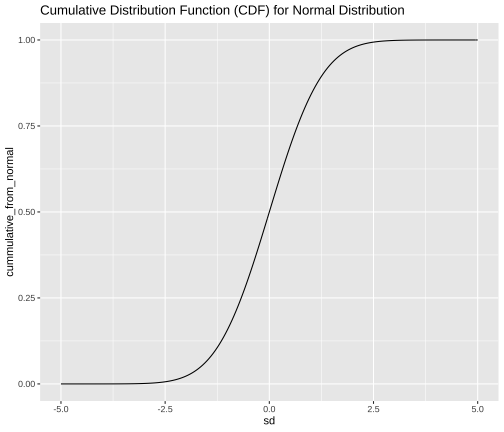<!-- --> ] <style> .panel1-dnorm_pnorm-auto { color: black; width: 38.6060606060606%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel2-dnorm_pnorm-auto { color: black; width: 59.3939393939394%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel3-dnorm_pnorm-auto { color: black; width: NA%; hight: 33%; float: left; padding-left: 1%; font-size: 80% } </style> --- # Using `prop.test()` function ### Is the proportion of Yuks is .25? ```r prop.test(x = 13, # number "successes" observed n = 15, # total number p = .25, # proportion expected under null alternative = # which extremes count "two.sided", # other options are greater and less correct = F) # use classic prop test ``` ``` 1-sample proportions test without continuity correction data: 13 out of 15, null probability 0.25 X-squared = 30.422, df = 1, p-value = 0.00000003475 alternative hypothesis: true p is not equal to 0.25 95 percent confidence interval: 0.6211802 0.9626387 sample estimates: p 0.8666667 ``` --- # Boxing ```r prop.test(x = 248, # number observed "successes" n = 457, # total number p = .5, # proportion expected under null alternative = # which extremes count "two.sided", # other options are greater and less correct = F) # use classic prop test ``` ``` 1-sample proportions test without continuity correction data: 248 out of 457, null probability 0.5 X-squared = 3.3282, df = 1, p-value = 0.0681 alternative hypothesis: true p is not equal to 0.5 95 percent confidence interval: 0.4968289 0.5877989 sample estimates: p 0.5426696 ```