This book looks some basic statistics: - covariance - variance - standard deviation - correlation coefficient --- We'll look at the *population* statistics first equation over all: --- class: inverse, center, middle # Covariance --- class: center, middle ### Covariance is a measure of the joint variability of two random variables. --- class: inverse, center, middle .huge[ $$ cov(x,y) = \frac{\sum_{i=1}^n (x_i-\mu_x)(y_i-\mu_y)}{n} $$ ] --- count: false .panel1-cov_steps-auto[ ## `$$(x_i, y_i)$$` ] .panel2-cov_steps-auto[ ``` r *datasaurus_dozen |> filter(dataset == "dino") |> ggplot() + aes(x = x, y = y) + geom_point() ``` ] .panel3-cov_steps-auto[ 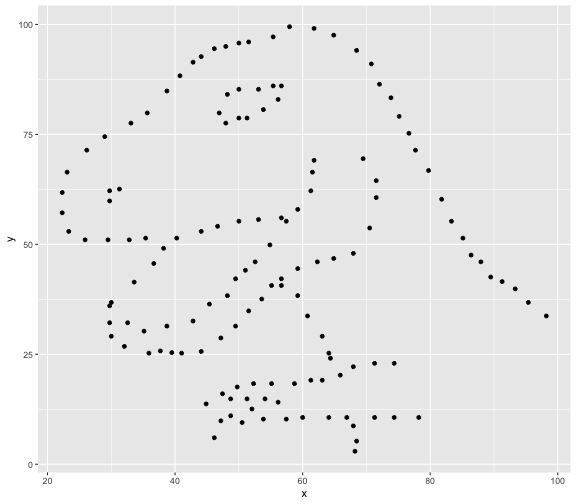<!-- --> ] --- count: false .panel1-cov_steps-auto[ ## `$$\bar{x}$$` ] .panel2-cov_steps-auto[ ``` r datasaurus_dozen |> filter(dataset == "dino") |> ggplot() + aes(x = x, y = y) + geom_point() + * geom_xmean() ``` ] .panel3-cov_steps-auto[ 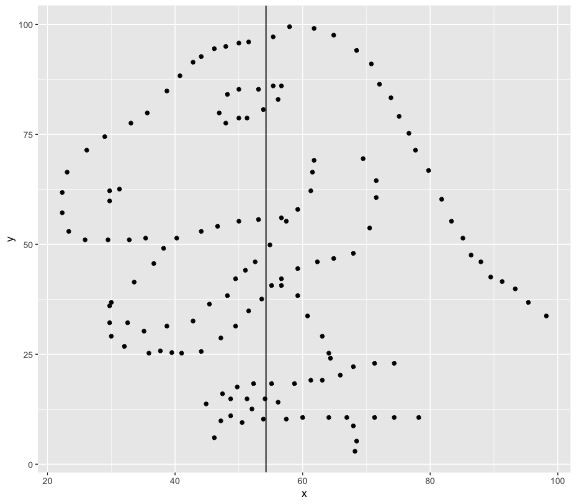<!-- --> ] --- count: false .panel1-cov_steps-auto[ ## `$$\bar{y}$$` ] .panel2-cov_steps-auto[ ``` r datasaurus_dozen |> filter(dataset == "dino") |> ggplot() + aes(x = x, y = y) + geom_point() + geom_xmean() + * geom_ymean() ``` ] .panel3-cov_steps-auto[ 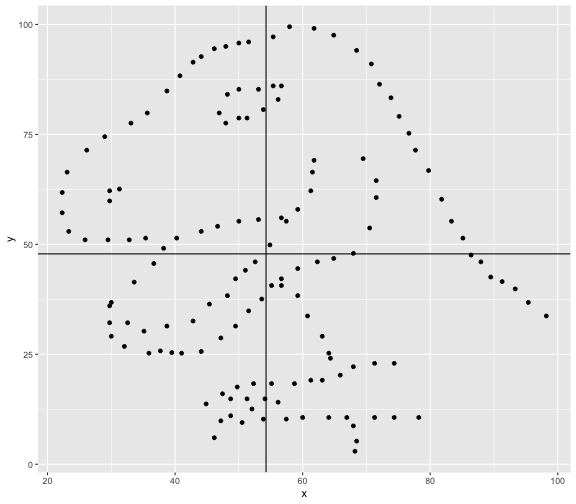<!-- --> ] --- count: false .panel1-cov_steps-auto[ ## `$$x_i-\bar{x}$$` ] .panel2-cov_steps-auto[ ``` r datasaurus_dozen |> filter(dataset == "dino") |> ggplot() + aes(x = x, y = y) + geom_point() + geom_xmean() + geom_ymean() + * geom_xmeandiff() ``` ] .panel3-cov_steps-auto[ 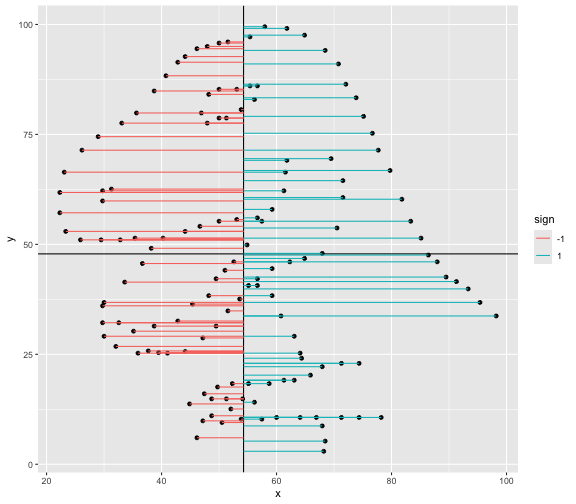<!-- --> ] --- count: false .panel1-cov_steps-auto[ ## `$$y_i-\bar{y}$$` ] .panel2-cov_steps-auto[ ``` r datasaurus_dozen |> filter(dataset == "dino") |> ggplot() + aes(x = x, y = y) + geom_point() + geom_xmean() + geom_ymean() + geom_xmeandiff() + * geom_ymeandiff() ``` ] .panel3-cov_steps-auto[ 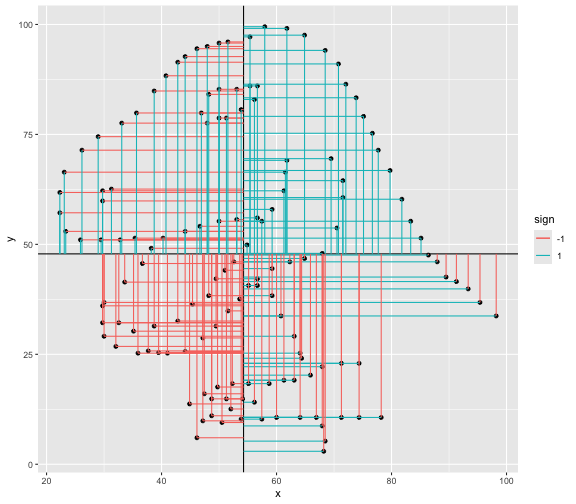<!-- --> ] --- count: false .panel1-cov_steps-auto[ ### `$$\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})$$` ] .panel2-cov_steps-auto[ ``` r datasaurus_dozen |> filter(dataset == "dino") |> ggplot() + aes(x = x, y = y) + geom_point() + geom_xmean() + geom_ymean() + geom_xmeandiff() + geom_ymeandiff() + * geom_xydiffs() ``` ] .panel3-cov_steps-auto[ 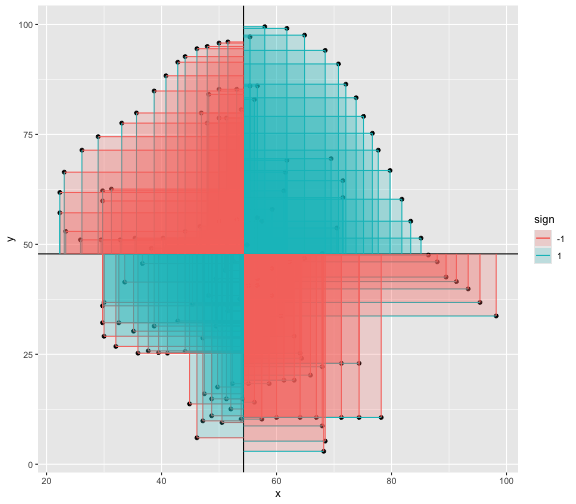<!-- --> ] --- count: false .panel1-cov_steps-auto[ ### `$$\frac{\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{n - 1}$$` ] .panel2-cov_steps-auto[ ``` r datasaurus_dozen |> filter(dataset == "dino") |> ggplot() + aes(x = x, y = y) + geom_point() + geom_xmean() + geom_ymean() + geom_xmeandiff() + geom_ymeandiff() + geom_xydiffs() + * geom_covariance() ``` ] .panel3-cov_steps-auto[ 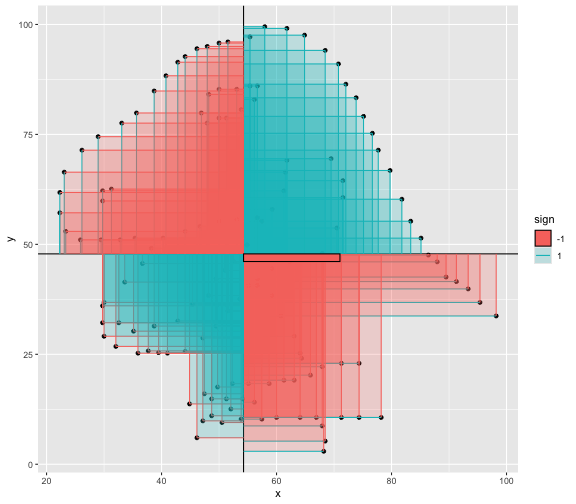<!-- --> ] --- count: false .panel1-cov_steps-auto[ ### `$$\frac{\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{n - 1}$$` ] .panel2-cov_steps-auto[ ``` r datasaurus_dozen |> filter(dataset == "dino") |> ggplot() + aes(x = x, y = y) + geom_point() + geom_xmean() + geom_ymean() + geom_xmeandiff() + geom_ymeandiff() + geom_xydiffs() + geom_covariance() + * geom_covariance_label() ``` ] .panel3-cov_steps-auto[ 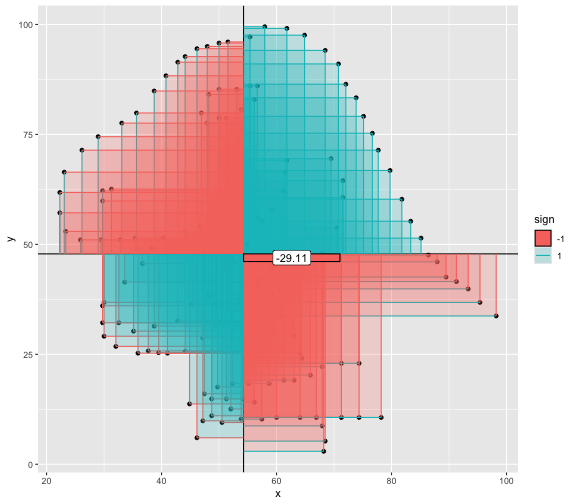<!-- --> ] --- count: false .panel1-cov_steps-auto[ ### `$$\frac{\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{n - 1}$$` ] .panel2-cov_steps-auto[ ``` r datasaurus_dozen |> filter(dataset == "dino") |> ggplot() + aes(x = x, y = y) + geom_point() + geom_xmean() + geom_ymean() + geom_xmeandiff() + geom_ymeandiff() + geom_xydiffs() + geom_covariance() + geom_covariance_label() + * labs(title = "Picture of covariance") ``` ] .panel3-cov_steps-auto[ 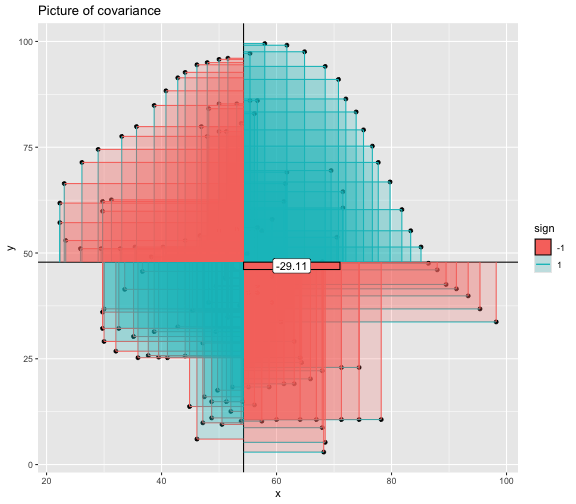<!-- --> ] --- count: false .panel1-cov_steps-auto[ ### `$$\frac{\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{n - 1}$$` ] .panel2-cov_steps-auto[ ``` r datasaurus_dozen |> filter(dataset == "dino") |> ggplot() + aes(x = x, y = y) + geom_point() + geom_xmean() + geom_ymean() + geom_xmeandiff() + geom_ymeandiff() + geom_xydiffs() + geom_covariance() + geom_covariance_label() + labs(title = "Picture of covariance") -> *xy_covariance ``` ] .panel3-cov_steps-auto[ ] <style> .panel1-cov_steps-auto { color: black; width: 32.3333333333333%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel2-cov_steps-auto { color: black; width: 32.3333333333333%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel3-cov_steps-auto { color: black; width: 32.3333333333333%; hight: 33%; float: left; padding-left: 1%; font-size: 80% } </style> --- class: inverse, middle, center # Variance and Standard Deviation --- class: inverse, center, middle .huge[ $$ var(x) = \frac{\sum_{i=1}^n (x_i-\mu_x)^2}{n - 1} $$ ] --- class: inverse, center, middle .huge[ $$ \sigma^2 = \frac{\sum_{i=1}^n (x_i-\mu_x)^2}{n - 1} $$ ] --- count: false .panel1-variance_steps-auto[ ### `$$\frac{\sum_{i=1}^n (x_i-\bar{x})(y_i-\bar{y})}{n - 1}$$` ] .panel2-variance_steps-auto[ ``` r *xy_covariance ``` ] .panel3-variance_steps-auto[ 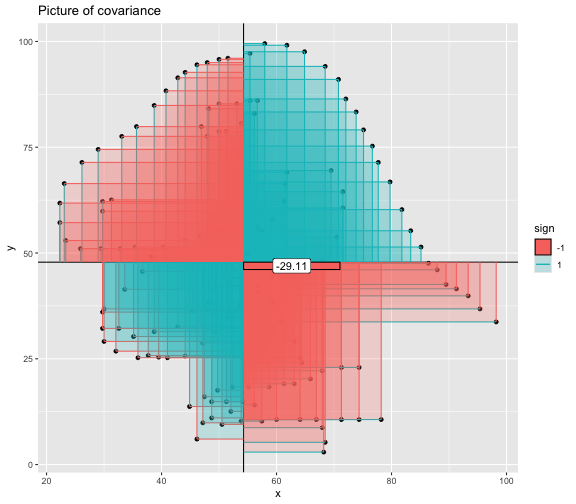<!-- --> ] --- count: false .panel1-variance_steps-auto[ ### `$$\frac{\sum_{i=1}^n (x_i-\bar{x})(x_i-\bar{x})}{n - 1}$$` ] .panel2-variance_steps-auto[ ``` r xy_covariance + * aes(y = x) ``` ] .panel3-variance_steps-auto[ 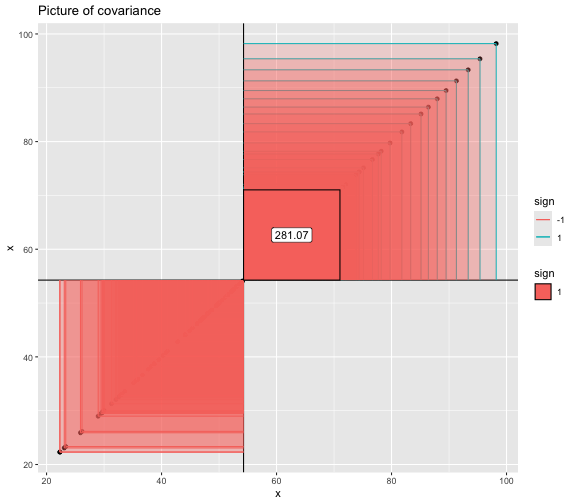<!-- --> ] --- count: false .panel1-variance_steps-auto[ ## `$$\frac{\sum_{i=1}^n (x_i-\mu_x)^2}{n - 1}$$` ] .panel2-variance_steps-auto[ ``` r xy_covariance + aes(y = x) + * labs(title = "Picture of Variance") ``` ] .panel3-variance_steps-auto[ 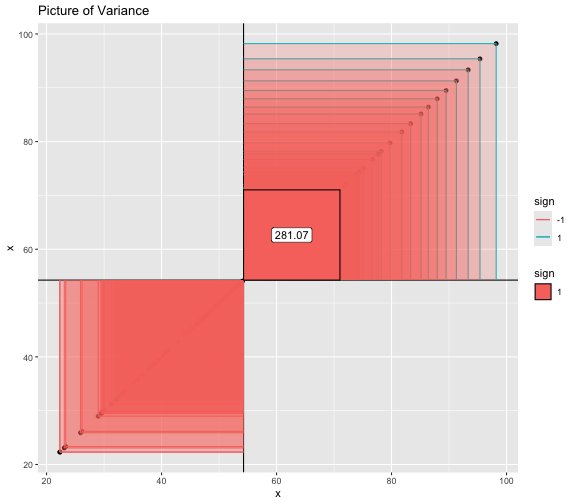<!-- --> ] --- count: false .panel1-variance_steps-auto[ NA ] .panel2-variance_steps-auto[ ``` r xy_covariance + aes(y = x) + labs(title = "Picture of Variance") + * geom_x_sd() ``` ] .panel3-variance_steps-auto[ 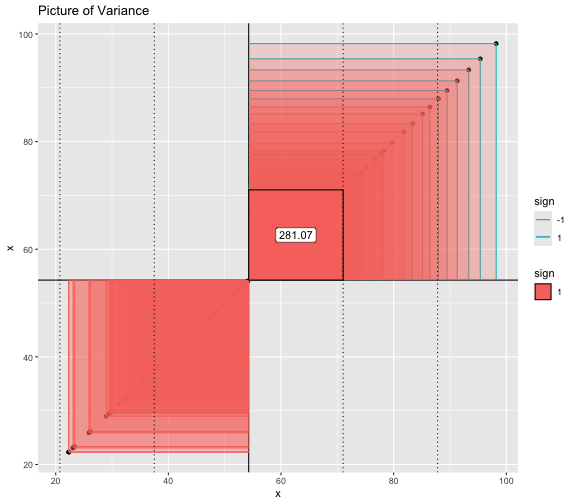<!-- --> ] --- count: false .panel1-variance_steps-auto[ NA ] .panel2-variance_steps-auto[ ``` r xy_covariance + aes(y = x) + labs(title = "Picture of Variance") + geom_x_sd() + * labs(title = "Picture of Variance & Standard Deviation") ``` ] .panel3-variance_steps-auto[ 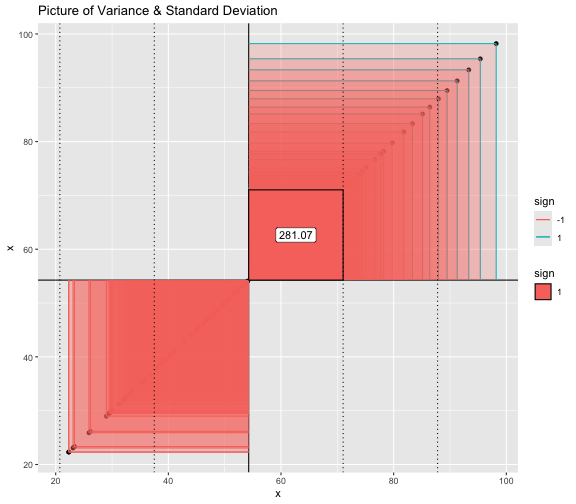<!-- --> ] --- count: false .panel1-variance_steps-auto[ NA ] .panel2-variance_steps-auto[ ``` r xy_covariance + aes(y = x) + labs(title = "Picture of Variance") + geom_x_sd() + labs(title = "Picture of Variance & Standard Deviation") -> *xx_variance_sd ``` ] .panel3-variance_steps-auto[ ] <style> .panel1-variance_steps-auto { color: black; width: 28.7040816326531%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel2-variance_steps-auto { color: black; width: 38.6020408163265%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel3-variance_steps-auto { color: black; width: 29.6938775510204%; hight: 33%; float: left; padding-left: 1%; font-size: 80% } </style> --- class: inverse, center, middle .huge[ $$ \sigma^2 = \frac{\sum_{i=1}^n (x_i-\mu_x)^2}{n - 1} $$ ] --- class: inverse, center, middle .huge[ $$ \sigma = \sqrt\frac{\sum_{i=1}^n (x_i-\mu_x)^2}{n - 1} $$ ] --- count: false .panel1-sd_steps-auto[ #### `$$\frac{\sum_{i=1}^n (x_i-\mu_x)^2}{n - 1}$$` ] .panel2-sd_steps-auto[ ``` r *xx_variance_sd ``` ] .panel3-sd_steps-auto[ 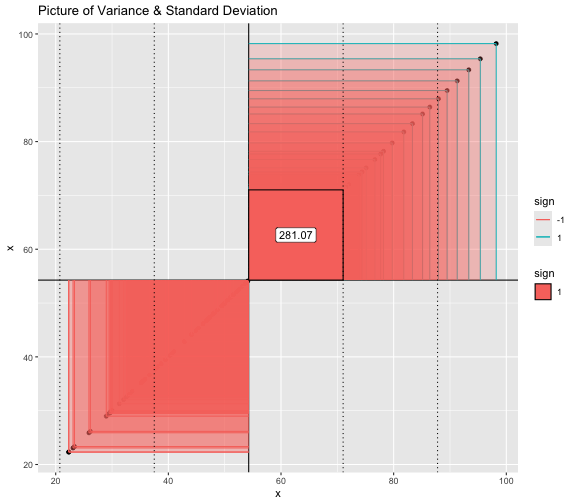<!-- --> ] --- count: false .panel1-sd_steps-auto[ #### `$$\sqrt\frac{\sum_{i=1}^n (x_i-\mu_x)^2}{n - 1}$$` ] .panel2-sd_steps-auto[ ``` r xx_variance_sd + * aes(y = y) ``` ] .panel3-sd_steps-auto[ 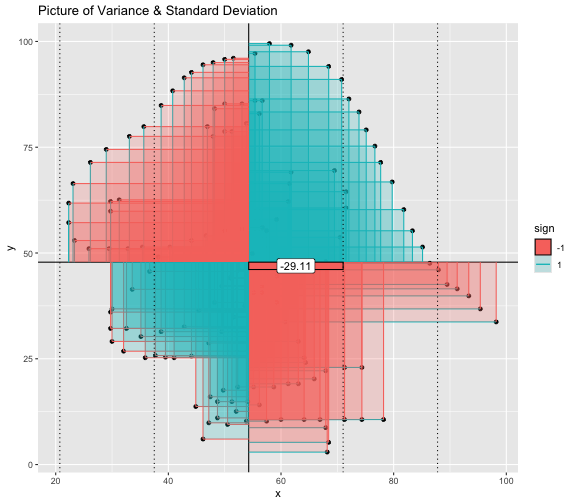<!-- --> ] --- count: false .panel1-sd_steps-auto[ NA ] .panel2-sd_steps-auto[ ``` r xx_variance_sd + aes(y = y) + * geom_y_sd() ``` ] .panel3-sd_steps-auto[ 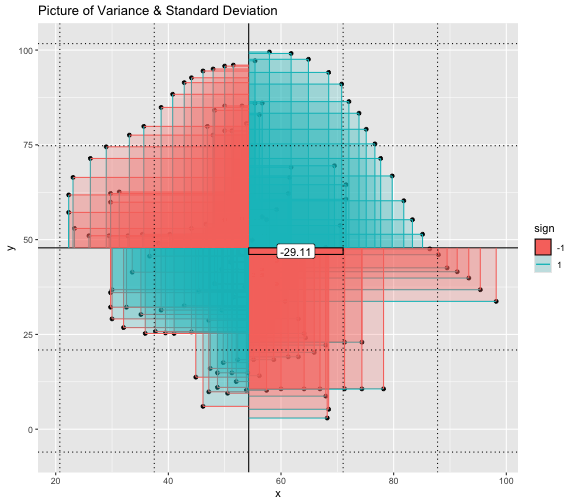<!-- --> ] --- count: false .panel1-sd_steps-auto[ NA ] .panel2-sd_steps-auto[ ``` r xx_variance_sd + aes(y = y) + geom_y_sd() + * aes(x = x/sd(x), * y = y/sd(y)) ``` ] .panel3-sd_steps-auto[ <!-- --> ] --- count: false .panel1-sd_steps-auto[ NA ] .panel2-sd_steps-auto[ ``` r xx_variance_sd + aes(y = y) + geom_y_sd() + aes(x = x/sd(x), y = y/sd(y)) + * labs(title = "Picture of Pearson correlation") ``` ] .panel3-sd_steps-auto[ <!-- --> ] <style> .panel1-sd_steps-auto { color: black; width: 28.7040816326531%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel2-sd_steps-auto { color: black; width: 38.6020408163265%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel3-sd_steps-auto { color: black; width: 29.6938775510204%; hight: 33%; float: left; padding-left: 1%; font-size: 80% } </style> ---  Creative commons, Wikipedia, M. W. Toews - Own work, based (in concept) on figure by Jeremy Kemp, on 2005-02-09 --- class: inverse, middle, center # correlation coefficient --- class: inverse, center, middle .huge[ $$ cor(x,y) = \frac{\sum_{i=1}^n (x_i-\mu_x)(y_i-\mu_y)}{n *\sigma_x \sigma_y} $$ ] --- count: false .panel1-cor_steps-user[ ## `$$\frac{\sum_{i=1}^n (x_i-\mu_x)(y_i-\mu_y)}{n - 1}$$` ] .panel2-cor_steps-user[ <!-- --> ] --- count: false .panel1-cor_steps-user[ ## `$$\frac{\sum_{i=1}^n (x_i-\mu_x)(y_i-\mu_y)}{n*\sigma_x}$$` ] .panel2-cor_steps-user[ <!-- --> ] --- count: false .panel1-cor_steps-user[ ## `$$\frac{\sum_{i=1}^n (x_i-\mu_x)(y_i-\mu_y)}{n*\sigma_x\sigma_y}$$` ] .panel2-cor_steps-user[ <!-- --> ] <style> .panel1-cor_steps-user { color: black; width: 43.5555555555556%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel2-cor_steps-user { color: black; width: 54.4444444444444%; hight: 32%; float: left; padding-left: 1%; font-size: 80% } .panel3-cor_steps-user { color: black; width: NA%; hight: 33%; float: left; padding-left: 1%; font-size: 80% } </style> --- # Bessel correction: n - 1 *Sample* statistics (Not *population* statistics) --- class: inverse, center, middle .huge[ $$ cov(x,y) = \frac{\sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n - 1} $$ ] --- class: inverse, center, middle .huge[ $$ s^2 = \frac{\sum_{i=1}^n (x_i-\overline{x})^2}{n - 1} $$ ] --- class: inverse, center, middle .huge[ $$ s = \sqrt\frac{\sum_{i=1}^n (x_i-\overline{x})^2}{n - 1} $$ ] --- # DRY: Bonus -- ## "Don't repeat yourself" -- ## Writing and using functions --- ``` r # this is a temporary fix - a mysetseed <- set.seed ``` --- r chunk_reveal("cov_steps1")` --- r chunk_reveal("cov_steps2", display_type = c("code", "func", "output"), widths = c(27, 37, 32))` --- --- # DRY next level: writing and using packages - [A companion guide to Jim Hester’s, 'You can make an R package in 20 minutes'](https://evamaerey.github.io/package_in_20_minutes/package_in_20_minutes) --- r chunk_reveal("numeric")` --- <style type="text/css"> .remark-code{line-height: 1.5; font-size: 70%} .huge { font-size: 250%; } @media print { .has-continuation { display: block; } } </style>