class: center, middle, inverse, title-slide # ols ## made with flipbookr and xaringan ### Gina Reynolds, Jan 2020 --- --- class: split-40 count: false .column[.content[ ```r cars %>% ggplot() + labs(title = "Fitting an OLS model to data in ggplot2") + aes(x = speed) + aes(y = dist) + geom_point(color = "steelblue", size = 2) + geom_smooth(method = lm, se = F) ``` ]] .column[.content[ ``` `geom_smooth()` using formula 'y ~ x' ``` 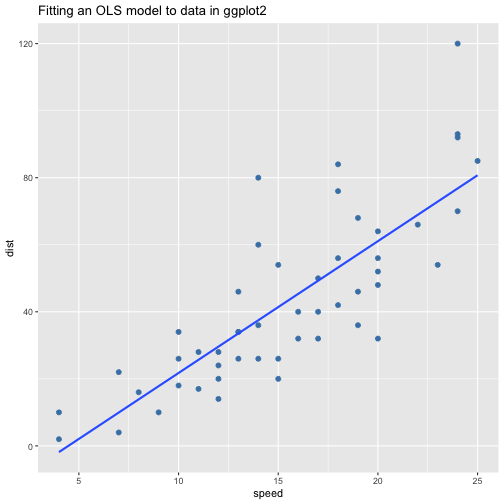<!-- --> ]] --- OLS in base R --- class: split-40 count: false .column[.content[ ```r # fitting a model *lm(formula = dist ~ speed, * data = cars) ``` ]] .column[.content[ ``` Call: lm(formula = dist ~ speed, data = cars) Coefficients: (Intercept) speed -17.579 3.932 ``` ]] --- class: split-40 count: false .column[.content[ ```r # fitting a model lm(formula = dist ~ speed, data = cars) -> *cars_model ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r # fitting a model lm(formula = dist ~ speed, data = cars) -> cars_model *# using summary() to # using summary() to ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r # fitting a model lm(formula = dist ~ speed, data = cars) -> cars_model # using summary() to # using summary() to # to pull out more info *cars_model ``` ]] .column[.content[ ``` Call: lm(formula = dist ~ speed, data = cars) Coefficients: (Intercept) speed -17.579 3.932 ``` ]] --- class: split-40 count: false .column[.content[ ```r # fitting a model lm(formula = dist ~ speed, data = cars) -> cars_model # using summary() to # using summary() to # to pull out more info cars_model %>% * summary() ``` ]] .column[.content[ ``` Call: lm(formula = dist ~ speed, data = cars) Residuals: Min 1Q Median 3Q Max -29.069 -9.525 -2.272 9.215 43.201 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -17.5791 6.7584 -2.601 0.0123 * speed 3.9324 0.4155 9.464 1.49e-12 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 Residual standard error: 15.38 on 48 degrees of freedom Multiple R-squared: 0.6511, Adjusted R-squared: 0.6438 F-statistic: 89.57 on 1 and 48 DF, p-value: 1.49e-12 ``` ]] --- class: split-40 count: false .column[.content[ ```r # fitting a model lm(formula = dist ~ speed, data = cars) -> cars_model # using summary() to # using summary() to # to pull out more info cars_model %>% summary() %>% * .$residuals ``` ]] .column[.content[ ``` 1 2 3 4 5 6 7 3.849460 11.849460 -5.947766 12.052234 2.119825 -7.812584 -3.744993 8 9 10 11 12 13 14 4.255007 12.255007 -8.677401 2.322599 -15.609810 -9.609810 -5.609810 15 16 17 18 19 20 21 -1.609810 -7.542219 0.457781 0.457781 12.457781 -11.474628 -1.474628 22 23 24 25 26 27 28 22.525372 42.525372 -21.407036 -15.407036 12.592964 -13.339445 -5.339445 29 30 31 32 33 34 35 -17.271854 -9.271854 0.728146 -11.204263 2.795737 22.795737 30.795737 36 37 38 39 40 41 42 -21.136672 -11.136672 10.863328 -29.069080 -13.069080 -9.069080 -5.069080 43 44 45 46 47 48 49 2.930920 -2.933898 -18.866307 -6.798715 15.201285 16.201285 43.201285 50 4.268876 ``` ]] --- # But {broom} is cool ... -- ...anticipating that we might want lots of this info pulled out systematically as data frames -- Broom returns dataframes at 3 levels - broom::glance(), overall model statistics - broom::tidy(), covariate level model statistics - broom::augment(), observation level statistics --- # *Model* level stats ```r cars_model %>% broom::glance() ``` ``` # A tibble: 1 x 11 r.squared adj.r.squared sigma statistic p.value df logLik AIC BIC <dbl> <dbl> <dbl> <dbl> <dbl> <int> <dbl> <dbl> <dbl> 1 0.651 0.644 15.4 89.6 1.49e-12 2 -207. 419. 425. # … with 2 more variables: deviance <dbl>, df.residual <int> ``` --- # *Covariate* level stats ```r cars_model %>% broom::tidy() ``` ``` # A tibble: 2 x 5 term estimate std.error statistic p.value <chr> <dbl> <dbl> <dbl> <dbl> 1 (Intercept) -17.6 6.76 -2.60 1.23e- 2 2 speed 3.93 0.416 9.46 1.49e-12 ``` --- # *Observation* level ```r cars_model %>% broom::augment() ``` ``` # A tibble: 50 x 9 dist speed .fitted .se.fit .resid .hat .sigma .cooksd .std.resid <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 2 4 -1.85 5.21 3.85 0.115 15.5 0.00459 0.266 2 10 4 -1.85 5.21 11.8 0.115 15.4 0.0435 0.819 3 4 7 9.95 4.11 -5.95 0.0715 15.5 0.00620 -0.401 4 22 7 9.95 4.11 12.1 0.0715 15.4 0.0255 0.813 5 16 8 13.9 3.77 2.12 0.0600 15.5 0.000645 0.142 6 10 9 17.8 3.44 -7.81 0.0499 15.5 0.00713 -0.521 7 18 10 21.7 3.12 -3.74 0.0413 15.5 0.00133 -0.249 8 26 10 21.7 3.12 4.26 0.0413 15.5 0.00172 0.283 9 34 10 21.7 3.12 12.3 0.0413 15.4 0.0143 0.814 10 17 11 25.7 2.84 -8.68 0.0341 15.5 0.00582 -0.574 # … with 40 more rows ``` --- `broom::augment()` is good for plotting those residuals and fitted values, and checking model assumptions. --- class: split-40 count: false .column[.content[ ```r *cars_model ``` ]] .column[.content[ ``` Call: lm(formula = dist ~ speed, data = cars) Coefficients: (Intercept) speed -17.579 3.932 ``` ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% * broom::augment() ``` ]] .column[.content[ ``` # A tibble: 50 x 9 dist speed .fitted .se.fit .resid .hat .sigma .cooksd .std.resid <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 2 4 -1.85 5.21 3.85 0.115 15.5 0.00459 0.266 2 10 4 -1.85 5.21 11.8 0.115 15.4 0.0435 0.819 3 4 7 9.95 4.11 -5.95 0.0715 15.5 0.00620 -0.401 4 22 7 9.95 4.11 12.1 0.0715 15.4 0.0255 0.813 5 16 8 13.9 3.77 2.12 0.0600 15.5 0.000645 0.142 6 10 9 17.8 3.44 -7.81 0.0499 15.5 0.00713 -0.521 7 18 10 21.7 3.12 -3.74 0.0413 15.5 0.00133 -0.249 8 26 10 21.7 3.12 4.26 0.0413 15.5 0.00172 0.283 9 34 10 21.7 3.12 12.3 0.0413 15.4 0.0143 0.814 10 17 11 25.7 2.84 -8.68 0.0341 15.5 0.00582 -0.574 # … with 40 more rows ``` ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% * ggplot() ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + * labs(title = "Plot of model fit") ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Plot of model fit") + * aes(x = speed) ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Plot of model fit") + aes(x = speed) + * aes(y = dist) ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Plot of model fit") + aes(x = speed) + aes(y = dist) + * geom_point(col = "steelblue") ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Plot of model fit") + aes(x = speed) + aes(y = dist) + geom_point(col = "steelblue") + * geom_smooth(method = lm, se = F) ``` ]] .column[.content[ ``` `geom_smooth()` using formula 'y ~ x' ``` <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Plot of model fit") + aes(x = speed) + aes(y = dist) + geom_point(col = "steelblue") + geom_smooth(method = lm, se = F) + * geom_point(aes(y = .fitted)) ``` ]] .column[.content[ ``` `geom_smooth()` using formula 'y ~ x' ``` <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Plot of model fit") + aes(x = speed) + aes(y = dist) + geom_point(col = "steelblue") + geom_smooth(method = lm, se = F) + geom_point(aes(y = .fitted)) + * aes(xend = speed) ``` ]] .column[.content[ ``` `geom_smooth()` using formula 'y ~ x' ``` <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Plot of model fit") + aes(x = speed) + aes(y = dist) + geom_point(col = "steelblue") + geom_smooth(method = lm, se = F) + geom_point(aes(y = .fitted)) + aes(xend = speed) + * aes(yend = .fitted) ``` ]] .column[.content[ ``` `geom_smooth()` using formula 'y ~ x' ``` <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Plot of model fit") + aes(x = speed) + aes(y = dist) + geom_point(col = "steelblue") + geom_smooth(method = lm, se = F) + geom_point(aes(y = .fitted)) + aes(xend = speed) + aes(yend = .fitted) + * geom_segment(color = "red", * linetype = "dashed") ``` ]] .column[.content[ ``` `geom_smooth()` using formula 'y ~ x' ``` 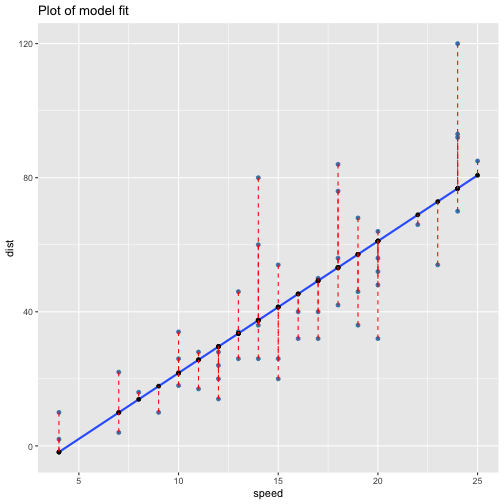<!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Plot of model fit") + aes(x = speed) + aes(y = dist) + geom_point(col = "steelblue") + geom_smooth(method = lm, se = F) + geom_point(aes(y = .fitted)) + aes(xend = speed) + aes(yend = .fitted) + geom_segment(color = "red", linetype = "dashed") + # input value of 21 miles per hour * geom_vline(xintercept = 21, * linetype = "dotted") ``` ]] .column[.content[ ``` `geom_smooth()` using formula 'y ~ x' ``` 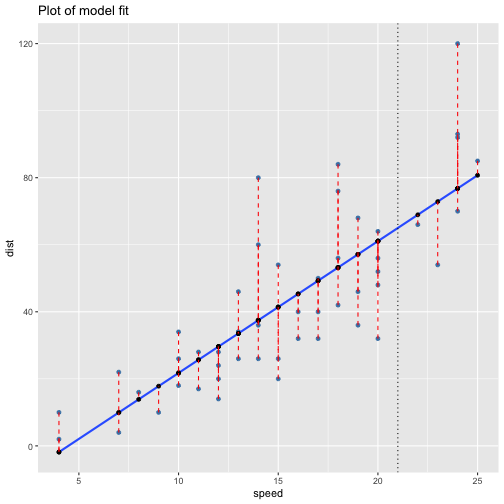<!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Plot of model fit") + aes(x = speed) + aes(y = dist) + geom_point(col = "steelblue") + geom_smooth(method = lm, se = F) + geom_point(aes(y = .fitted)) + aes(xend = speed) + aes(yend = .fitted) + geom_segment(color = "red", linetype = "dashed") + # input value of 21 miles per hour geom_vline(xintercept = 21, linetype = "dotted") + # yields predicted for y, stopping distance * geom_hline(yintercept = * predict(cars_model, * data.frame(speed = 21)), * linetype = "dotted") ``` ]] .column[.content[ ``` `geom_smooth()` using formula 'y ~ x' ``` 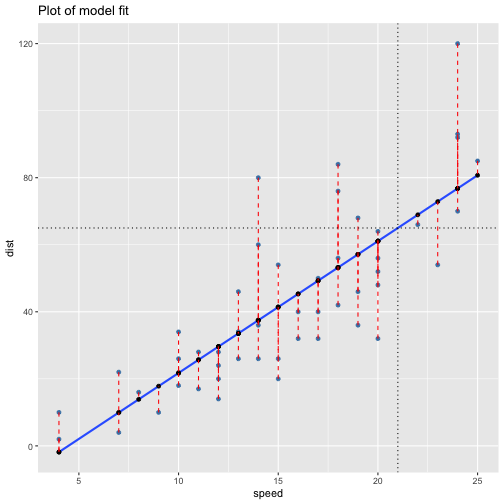<!-- --> ]] --- Checking assumption: residuals not correlated with predictions... --- class: split-40 count: false .column[.content[ ```r *cars_model ``` ]] .column[.content[ ``` Call: lm(formula = dist ~ speed, data = cars) Coefficients: (Intercept) speed -17.579 3.932 ``` ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% * broom::augment() ``` ]] .column[.content[ ``` # A tibble: 50 x 9 dist speed .fitted .se.fit .resid .hat .sigma .cooksd .std.resid <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 2 4 -1.85 5.21 3.85 0.115 15.5 0.00459 0.266 2 10 4 -1.85 5.21 11.8 0.115 15.4 0.0435 0.819 3 4 7 9.95 4.11 -5.95 0.0715 15.5 0.00620 -0.401 4 22 7 9.95 4.11 12.1 0.0715 15.4 0.0255 0.813 5 16 8 13.9 3.77 2.12 0.0600 15.5 0.000645 0.142 6 10 9 17.8 3.44 -7.81 0.0499 15.5 0.00713 -0.521 7 18 10 21.7 3.12 -3.74 0.0413 15.5 0.00133 -0.249 8 26 10 21.7 3.12 4.26 0.0413 15.5 0.00172 0.283 9 34 10 21.7 3.12 12.3 0.0413 15.4 0.0143 0.814 10 17 11 25.7 2.84 -8.68 0.0341 15.5 0.00582 -0.574 # … with 40 more rows ``` ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% * ggplot() ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + * labs(title = "Residuals v. Fitted") ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Residuals v. Fitted") + * aes(x = .fitted) ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Residuals v. Fitted") + aes(x = .fitted) + * aes(y = .resid) ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Residuals v. Fitted") + aes(x = .fitted) + aes(y = .resid) + * geom_point(col = "steelblue") ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Residuals v. Fitted") + aes(x = .fitted) + aes(y = .resid) + geom_point(col = "steelblue") + * geom_hline(yintercept = 0, * lty = "dashed") ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% ggplot() + labs(title = "Residuals v. Fitted") + aes(x = .fitted) + aes(y = .resid) + geom_point(col = "steelblue") + geom_hline(yintercept = 0, lty = "dashed") + * geom_smooth(se = F, span = 1, * color = "red") ``` ]] .column[.content[ ``` `geom_smooth()` using method = 'loess' and formula 'y ~ x' ``` <!-- --> ]] --- # Checking for outliers with Cook's distance --- class: split-40 count: false .column[.content[ ```r *cars_model ``` ]] .column[.content[ ``` Call: lm(formula = dist ~ speed, data = cars) Coefficients: (Intercept) speed -17.579 3.932 ``` ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% * broom::augment() ``` ]] .column[.content[ ``` # A tibble: 50 x 9 dist speed .fitted .se.fit .resid .hat .sigma .cooksd .std.resid <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 2 4 -1.85 5.21 3.85 0.115 15.5 0.00459 0.266 2 10 4 -1.85 5.21 11.8 0.115 15.4 0.0435 0.819 3 4 7 9.95 4.11 -5.95 0.0715 15.5 0.00620 -0.401 4 22 7 9.95 4.11 12.1 0.0715 15.4 0.0255 0.813 5 16 8 13.9 3.77 2.12 0.0600 15.5 0.000645 0.142 6 10 9 17.8 3.44 -7.81 0.0499 15.5 0.00713 -0.521 7 18 10 21.7 3.12 -3.74 0.0413 15.5 0.00133 -0.249 8 26 10 21.7 3.12 4.26 0.0413 15.5 0.00172 0.283 9 34 10 21.7 3.12 12.3 0.0413 15.4 0.0143 0.814 10 17 11 25.7 2.84 -8.68 0.0341 15.5 0.00582 -0.574 # … with 40 more rows ``` ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% * mutate(id = row_number()) ``` ]] .column[.content[ ``` # A tibble: 50 x 10 dist speed .fitted .se.fit .resid .hat .sigma .cooksd .std.resid id <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <int> 1 2 4 -1.85 5.21 3.85 0.115 15.5 0.00459 0.266 1 2 10 4 -1.85 5.21 11.8 0.115 15.4 0.0435 0.819 2 3 4 7 9.95 4.11 -5.95 0.0715 15.5 0.00620 -0.401 3 4 22 7 9.95 4.11 12.1 0.0715 15.4 0.0255 0.813 4 5 16 8 13.9 3.77 2.12 0.0600 15.5 0.000645 0.142 5 6 10 9 17.8 3.44 -7.81 0.0499 15.5 0.00713 -0.521 6 7 18 10 21.7 3.12 -3.74 0.0413 15.5 0.00133 -0.249 7 8 26 10 21.7 3.12 4.26 0.0413 15.5 0.00172 0.283 8 9 34 10 21.7 3.12 12.3 0.0413 15.4 0.0143 0.814 9 10 17 11 25.7 2.84 -8.68 0.0341 15.5 0.00582 -0.574 10 # … with 40 more rows ``` ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(id = row_number()) %>% * ggplot() ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(id = row_number()) %>% ggplot() + * labs(title = "Cook's Distance, by ID (row number)") ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(id = row_number()) %>% ggplot() + labs(title = "Cook's Distance, by ID (row number)") + * labs(subtitle = "Cook's Distance, a measure of influence via a leave one out procedure") ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(id = row_number()) %>% ggplot() + labs(title = "Cook's Distance, by ID (row number)") + labs(subtitle = "Cook's Distance, a measure of influence via a leave one out procedure") + * aes(x = id) ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(id = row_number()) %>% ggplot() + labs(title = "Cook's Distance, by ID (row number)") + labs(subtitle = "Cook's Distance, a measure of influence via a leave one out procedure") + aes(x = id) + * aes(y = .cooksd) ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(id = row_number()) %>% ggplot() + labs(title = "Cook's Distance, by ID (row number)") + labs(subtitle = "Cook's Distance, a measure of influence via a leave one out procedure") + aes(x = id) + aes(y = .cooksd) + * geom_point() ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(id = row_number()) %>% ggplot() + labs(title = "Cook's Distance, by ID (row number)") + labs(subtitle = "Cook's Distance, a measure of influence via a leave one out procedure") + aes(x = id) + aes(y = .cooksd) + geom_point() + * aes(label = id) ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(id = row_number()) %>% ggplot() + labs(title = "Cook's Distance, by ID (row number)") + labs(subtitle = "Cook's Distance, a measure of influence via a leave one out procedure") + aes(x = id) + aes(y = .cooksd) + geom_point() + aes(label = id) + * geom_text(check_overlap = T, * nudge_y = .015) ``` ]] .column[.content[ 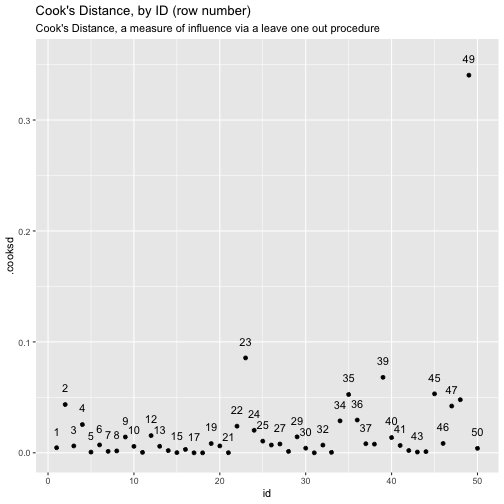<!-- --> ]] --- --- Are the residuals normally distributed? --- class: split-40 count: false .column[.content[ ```r *cars_model ``` ]] .column[.content[ ``` Call: lm(formula = dist ~ speed, data = cars) Coefficients: (Intercept) speed -17.579 3.932 ``` ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% * broom::augment() ``` ]] .column[.content[ ``` # A tibble: 50 x 9 dist speed .fitted .se.fit .resid .hat .sigma .cooksd .std.resid <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 2 4 -1.85 5.21 3.85 0.115 15.5 0.00459 0.266 2 10 4 -1.85 5.21 11.8 0.115 15.4 0.0435 0.819 3 4 7 9.95 4.11 -5.95 0.0715 15.5 0.00620 -0.401 4 22 7 9.95 4.11 12.1 0.0715 15.4 0.0255 0.813 5 16 8 13.9 3.77 2.12 0.0600 15.5 0.000645 0.142 6 10 9 17.8 3.44 -7.81 0.0499 15.5 0.00713 -0.521 7 18 10 21.7 3.12 -3.74 0.0413 15.5 0.00133 -0.249 8 26 10 21.7 3.12 4.26 0.0413 15.5 0.00172 0.283 9 34 10 21.7 3.12 12.3 0.0413 15.4 0.0143 0.814 10 17 11 25.7 2.84 -8.68 0.0341 15.5 0.00582 -0.574 # … with 40 more rows ``` ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% * mutate(expected = qnorm((1:n() - .5)/n())) ``` ]] .column[.content[ ``` # A tibble: 50 x 10 dist speed .fitted .se.fit .resid .hat .sigma .cooksd .std.resid expected <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> <dbl> 1 2 4 -1.85 5.21 3.85 0.115 15.5 0.00459 0.266 -2.33 2 10 4 -1.85 5.21 11.8 0.115 15.4 0.0435 0.819 -1.88 3 4 7 9.95 4.11 -5.95 0.0715 15.5 0.00620 -0.401 -1.64 4 22 7 9.95 4.11 12.1 0.0715 15.4 0.0255 0.813 -1.48 5 16 8 13.9 3.77 2.12 0.0600 15.5 0.000645 0.142 -1.34 6 10 9 17.8 3.44 -7.81 0.0499 15.5 0.00713 -0.521 -1.23 7 18 10 21.7 3.12 -3.74 0.0413 15.5 0.00133 -0.249 -1.13 8 26 10 21.7 3.12 4.26 0.0413 15.5 0.00172 0.283 -1.04 9 34 10 21.7 3.12 12.3 0.0413 15.4 0.0143 0.814 -0.954 10 17 11 25.7 2.84 -8.68 0.0341 15.5 0.00582 -0.574 -0.878 # … with 40 more rows ``` ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(expected = qnorm((1:n() - .5)/n())) %>% * ggplot() ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(expected = qnorm((1:n() - .5)/n())) %>% ggplot() + * labs(title = "Normal q-q plot") ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(expected = qnorm((1:n() - .5)/n())) %>% ggplot() + labs(title = "Normal q-q plot") + * aes(y = sort(.std.resid)) ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(expected = qnorm((1:n() - .5)/n())) %>% ggplot() + labs(title = "Normal q-q plot") + aes(y = sort(.std.resid)) + * aes(x = expected) ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(expected = qnorm((1:n() - .5)/n())) %>% ggplot() + labs(title = "Normal q-q plot") + aes(y = sort(.std.resid)) + aes(x = expected) + * geom_rug() ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(expected = qnorm((1:n() - .5)/n())) %>% ggplot() + labs(title = "Normal q-q plot") + aes(y = sort(.std.resid)) + aes(x = expected) + geom_rug() + * geom_point() ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(expected = qnorm((1:n() - .5)/n())) %>% ggplot() + labs(title = "Normal q-q plot") + aes(y = sort(.std.resid)) + aes(x = expected) + geom_rug() + geom_point() + * coord_equal(ratio = 1, * xlim = c(-4, 4), * ylim = c(-4, 4)) ``` ]] .column[.content[ <!-- --> ]] --- class: split-40 count: false .column[.content[ ```r cars_model %>% broom::augment() %>% mutate(expected = qnorm((1:n() - .5)/n())) %>% ggplot() + labs(title = "Normal q-q plot") + aes(y = sort(.std.resid)) + aes(x = expected) + geom_rug() + geom_point() + coord_equal(ratio = 1, xlim = c(-4, 4), ylim = c(-4, 4)) + # add line of equivilance * geom_abline(intercept = 0, * slope = 1, * linetype = "dotted") ``` ]] .column[.content[ <!-- --> ]] --- # ```r cars_model ``` ``` Call: lm(formula = dist ~ speed, data = cars) Coefficients: (Intercept) speed -17.579 3.932 ``` --- --- # multiple regression... -- ...and multiple models in a single table --- # subsetting to 2002 ```r library(gapminder) gapminder %>% filter(year == 2002) -> gapminder_2002 ``` --- class: split-40 count: false .column[.content[ ```r *lm(lifeExp ~ gdpPercap, * data = gapminder_2002) ``` ]] .column[.content[ ``` Call: lm(formula = lifeExp ~ gdpPercap, data = gapminder_2002) Coefficients: (Intercept) gdpPercap 5.825e+01 7.507e-04 ``` ]] --- class: split-40 count: false .column[.content[ ```r lm(lifeExp ~ gdpPercap, data = gapminder_2002) -> *model1 ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r lm(lifeExp ~ gdpPercap, data = gapminder_2002) -> model1 *lm(lifeExp ~ gdpPercap + pop, * data = gapminder_2002) ``` ]] .column[.content[ ``` Call: lm(formula = lifeExp ~ gdpPercap + pop, data = gapminder_2002) Coefficients: (Intercept) gdpPercap pop 5.789e+01 7.554e-04 7.516e-09 ``` ]] --- class: split-40 count: false .column[.content[ ```r lm(lifeExp ~ gdpPercap, data = gapminder_2002) -> model1 lm(lifeExp ~ gdpPercap + pop, data = gapminder_2002) -> *model2 ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r lm(lifeExp ~ gdpPercap, data = gapminder_2002) -> model1 lm(lifeExp ~ gdpPercap + pop, data = gapminder_2002) -> model2 *lm(lifeExp ~ gdpPercap + * continent, * data = gapminder_2002) ``` ]] .column[.content[ ``` Call: lm(formula = lifeExp ~ gdpPercap + continent, data = gapminder_2002) Coefficients: (Intercept) gdpPercap continentAmericas continentAsia 5.224e+01 4.168e-04 1.631e+01 1.275e+01 continentEurope continentOceania 1.541e+01 1.627e+01 ``` ]] --- class: split-40 count: false .column[.content[ ```r lm(lifeExp ~ gdpPercap, data = gapminder_2002) -> model1 lm(lifeExp ~ gdpPercap + pop, data = gapminder_2002) -> model2 lm(lifeExp ~ gdpPercap + continent, data = gapminder_2002) -> *model3 ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r lm(lifeExp ~ gdpPercap, data = gapminder_2002) -> model1 lm(lifeExp ~ gdpPercap + pop, data = gapminder_2002) -> model2 lm(lifeExp ~ gdpPercap + continent, data = gapminder_2002) -> model3 # *stargazer::stargazer( * model1, model2, model3, # if you want to work interactivevly, change "html" to "text" # note, chunk results option is "asis" * type = "text", * dep.var.labels = "Life Expectancy (years)", * covariate.labels = c("GDP per cap (Thousands $US)", * "Population (Millions)"), * style = "qje", * font.size = "small", * title = "Models of Life Expectancy in 2002") ``` ]] .column[.content[ ``` Models of Life Expectancy in 2002 =================================================================================================== Life Expectancy (years) (1) (2) (3) --------------------------------------------------------------------------------------------------- GDP per cap (Thousands US) 0.001*** 0.001*** 0.0004*** (0.0001) (0.0001) (0.0001) Population (Millions) 0.000 (0.000) continentAmericas 16.309*** (1.676) continentAsia 12.751*** (1.561) continentEurope 15.409*** (1.982) continentOceania 16.270*** (5.051) Constant 58.250*** 57.891*** 52.242*** (1.014) (1.043) (0.937) N 142 142 142 R2 0.465 0.472 0.718 Adjusted R2 0.461 0.465 0.708 Residual Std. Error 9.015 (df = 140) 8.984 (df = 139) 6.640 (df = 136) F Statistic 121.648*** (df = 1; 140) 62.214*** (df = 2; 139) 69.244*** (df = 5; 136) =================================================================================================== Notes: ***Significant at the 1 percent level. **Significant at the 5 percent level. *Significant at the 10 percent level. ``` ]] --- class: split-40 count: false .column[.content[ ```r lm(lifeExp ~ gdpPercap, data = gapminder_2002) -> model1 lm(lifeExp ~ gdpPercap + pop, data = gapminder_2002) -> model2 lm(lifeExp ~ gdpPercap + continent, data = gapminder_2002) -> model3 # stargazer::stargazer( model1, model2, model3, # if you want to work interactivevly, change "html" to "text" # note, chunk results option is "asis" type = "text", dep.var.labels = "Life Expectancy (years)", covariate.labels = c("GDP per cap (Thousands $US)", "Population (Millions)"), style = "qje", font.size = "small", title = "Models of Life Expectancy in 2002") -> *formatted_models_table ``` ]] .column[.content[ ``` Models of Life Expectancy in 2002 =================================================================================================== Life Expectancy (years) (1) (2) (3) --------------------------------------------------------------------------------------------------- GDP per cap (Thousands US) 0.001*** 0.001*** 0.0004*** (0.0001) (0.0001) (0.0001) Population (Millions) 0.000 (0.000) continentAmericas 16.309*** (1.676) continentAsia 12.751*** (1.561) continentEurope 15.409*** (1.982) continentOceania 16.270*** (5.051) Constant 58.250*** 57.891*** 52.242*** (1.014) (1.043) (0.937) N 142 142 142 R2 0.465 0.472 0.718 Adjusted R2 0.461 0.465 0.708 Residual Std. Error 9.015 (df = 140) 8.984 (df = 139) 6.640 (df = 136) F Statistic 121.648*** (df = 1; 140) 62.214*** (df = 2; 139) 69.244*** (df = 5; 136) =================================================================================================== Notes: ***Significant at the 1 percent level. **Significant at the 5 percent level. *Significant at the 10 percent level. ``` ]] --- if you change they `type` argument to "html", and the code chunk option to results = "asis" <table style="text-align:center"><caption><strong>Models of Life Expectancy in 2002</strong></caption> <tr><td colspan="4" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"></td><td colspan="3">Life Expectancy (years)</td></tr> <tr><td style="text-align:left"></td><td>(1)</td><td>(2)</td><td>(3)</td></tr> <tr><td colspan="4" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left">GDP per cap (Thousands US)</td><td>0.001^***</td><td>0.001^***</td><td>0.0004^***</td></tr> <tr><td style="text-align:left"></td><td>(0.0001)</td><td>(0.0001)</td><td>(0.0001)</td></tr> <tr><td style="text-align:left"></td><td></td><td></td><td></td></tr> <tr><td style="text-align:left">Population (Millions)</td><td></td><td>0.000</td><td></td></tr> <tr><td style="text-align:left"></td><td></td><td>(0.000)</td><td></td></tr> <tr><td style="text-align:left"></td><td></td><td></td><td></td></tr> <tr><td style="text-align:left">continentAmericas</td><td></td><td></td><td>16.309^***</td></tr> <tr><td style="text-align:left"></td><td></td><td></td><td>(1.676)</td></tr> <tr><td style="text-align:left"></td><td></td><td></td><td></td></tr> <tr><td style="text-align:left">continentAsia</td><td></td><td></td><td>12.751^***</td></tr> <tr><td style="text-align:left"></td><td></td><td></td><td>(1.561)</td></tr> <tr><td style="text-align:left"></td><td></td><td></td><td></td></tr> <tr><td style="text-align:left">continentEurope</td><td></td><td></td><td>15.409^***</td></tr> <tr><td style="text-align:left"></td><td></td><td></td><td>(1.982)</td></tr> <tr><td style="text-align:left"></td><td></td><td></td><td></td></tr> <tr><td style="text-align:left">continentOceania</td><td></td><td></td><td>16.270^***</td></tr> <tr><td style="text-align:left"></td><td></td><td></td><td>(5.051)</td></tr> <tr><td style="text-align:left"></td><td></td><td></td><td></td></tr> <tr><td style="text-align:left">Constant</td><td>58.250^***</td><td>57.891^***</td><td>52.242^***</td></tr> <tr><td style="text-align:left"></td><td>(1.014)</td><td>(1.043)</td><td>(0.937)</td></tr> <tr><td style="text-align:left"></td><td></td><td></td><td></td></tr> <tr><td style="text-align:left"><em>N</em></td><td>142</td><td>142</td><td>142</td></tr> <tr><td style="text-align:left">R²</td><td>0.465</td><td>0.472</td><td>0.718</td></tr> <tr><td style="text-align:left">Adjusted R²</td><td>0.461</td><td>0.465</td><td>0.708</td></tr> <tr><td style="text-align:left">Residual Std. Error</td><td>9.015 (df = 140)</td><td>8.984 (df = 139)</td><td>6.640 (df = 136)</td></tr> <tr><td style="text-align:left">F Statistic</td><td>121.648^*** (df = 1; 140)</td><td>62.214^*** (df = 2; 139)</td><td>69.244^*** (df = 5; 136)</td></tr> <tr><td colspan="4" style="border-bottom: 1px solid black"></td></tr><tr><td style="text-align:left"><em>Notes:</em></td><td colspan="3" style="text-align:right">^***Significant at the 1 percent level.</td></tr> <tr><td style="text-align:left"></td><td colspan="3" style="text-align:right">^**Significant at the 5 percent level.</td></tr> <tr><td style="text-align:left"></td><td colspan="3" style="text-align:right">^*Significant at the 10 percent level.</td></tr> </table> --- # the maths! --- class: split-40 count: false .column[.content[ ```r # create artificial data set # set seed for reproducibility *set.seed(501) ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r # create artificial data set # set seed for reproducibility set.seed(501) # head_size in cm *rnorm(n = 20, mean = 30, sd = 10) ``` ]] .column[.content[ ``` [1] 35.77281 36.17452 34.52007 32.25781 21.55195 15.66631 13.51793 30.35623 [9] 31.84019 42.23762 30.87002 39.05107 32.37906 34.65357 39.27268 28.10562 [17] 28.13692 40.97114 24.25709 36.85942 ``` ]] --- class: split-40 count: false .column[.content[ ```r # create artificial data set # set seed for reproducibility set.seed(501) # head_size in cm rnorm(n = 20, mean = 30, sd = 10) -> * head_size ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r # create artificial data set # set seed for reproducibility set.seed(501) # head_size in cm rnorm(n = 20, mean = 30, sd = 10) -> head_size # tail_length in kilogram the relationship between head_size # and tail_length is completely random *head_size ``` ]] .column[.content[ ``` [1] 35.77281 36.17452 34.52007 32.25781 21.55195 15.66631 13.51793 30.35623 [9] 31.84019 42.23762 30.87002 39.05107 32.37906 34.65357 39.27268 28.10562 [17] 28.13692 40.97114 24.25709 36.85942 ``` ]] --- class: split-40 count: false .column[.content[ ```r # create artificial data set # set seed for reproducibility set.seed(501) # head_size in cm rnorm(n = 20, mean = 30, sd = 10) -> head_size # tail_length in kilogram the relationship between head_size # and tail_length is completely random head_size * * rnorm(20, 0, sd = 15) ``` ]] .column[.content[ ``` [1] 617.94937 374.08845 78.60973 220.43739 -90.05541 -67.70514 [7] 212.59042 -236.91309 -630.04145 182.98154 288.24508 290.78784 [13] 267.12589 419.40205 878.78295 218.98375 -115.72531 5.63956 [19] -143.70412 -83.67543 ``` ]] --- class: split-40 count: false .column[.content[ ```r # create artificial data set # set seed for reproducibility set.seed(501) # head_size in cm rnorm(n = 20, mean = 30, sd = 10) -> head_size # tail_length in kilogram the relationship between head_size # and tail_length is completely random head_size * rnorm(20, 0, sd = 15) + * 80 ``` ]] .column[.content[ ``` [1] 697.949367 454.088447 158.609728 300.437392 -10.055414 12.294857 [7] 292.590425 -156.913095 -550.041452 262.981543 368.245079 370.787842 [13] 347.125890 499.402052 958.782945 298.983754 -35.725305 85.639560 [19] -63.704121 -3.675432 ``` ]] --- class: split-40 count: false .column[.content[ ```r # create artificial data set # set seed for reproducibility set.seed(501) # head_size in cm rnorm(n = 20, mean = 30, sd = 10) -> head_size # tail_length in kilogram the relationship between head_size # and tail_length is completely random head_size * rnorm(20, 0, sd = 15) + 80 -> *tail_length ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r # create artificial data set # set seed for reproducibility set.seed(501) # head_size in cm rnorm(n = 20, mean = 30, sd = 10) -> head_size # tail_length in kilogram the relationship between head_size # and tail_length is completely random head_size * rnorm(20, 0, sd = 15) + 80 -> tail_length # join head_size and tail_length in data frame *data.frame(head_size, tail_length) ``` ]] .column[.content[ ``` head_size tail_length 1 35.77281 697.949367 2 36.17452 454.088447 3 34.52007 158.609728 4 32.25781 300.437392 5 21.55195 -10.055414 6 15.66631 12.294857 7 13.51793 292.590425 8 30.35623 -156.913095 9 31.84019 -550.041452 10 42.23762 262.981543 11 30.87002 368.245079 12 39.05107 370.787842 13 32.37906 347.125890 14 34.65357 499.402052 15 39.27268 958.782945 16 28.10562 298.983754 17 28.13692 -35.725305 18 40.97114 85.639560 19 24.25709 -63.704121 20 36.85942 -3.675432 ``` ]] --- class: split-40 count: false .column[.content[ ```r # create artificial data set # set seed for reproducibility set.seed(501) # head_size in cm rnorm(n = 20, mean = 30, sd = 10) -> head_size # tail_length in kilogram the relationship between head_size # and tail_length is completely random head_size * rnorm(20, 0, sd = 15) + 80 -> tail_length # join head_size and tail_length in data frame data.frame(head_size, tail_length) -> * df ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r # create artificial data set # set seed for reproducibility set.seed(501) # head_size in cm rnorm(n = 20, mean = 30, sd = 10) -> head_size # tail_length in kilogram the relationship between head_size # and tail_length is completely random head_size * rnorm(20, 0, sd = 15) + 80 -> tail_length # join head_size and tail_length in data frame data.frame(head_size, tail_length) -> df *lm(tail_length ~ head_size, data = df) ``` ]] .column[.content[ ``` Call: lm(formula = tail_length ~ head_size, data = df) Coefficients: (Intercept) head_size -214.66 13.65 ``` ]] --- class: split-40 count: false .column[.content[ ```r # create artificial data set # set seed for reproducibility set.seed(501) # head_size in cm rnorm(n = 20, mean = 30, sd = 10) -> head_size # tail_length in kilogram the relationship between head_size # and tail_length is completely random head_size * rnorm(20, 0, sd = 15) + 80 -> tail_length # join head_size and tail_length in data frame data.frame(head_size, tail_length) -> df lm(tail_length ~ head_size, data = df) %>% * summary() ``` ]] .column[.content[ ``` Call: lm(formula = tail_length ~ head_size, data = df) Residuals: Min 1Q Median 3Q Max -770.13 -186.51 32.64 164.75 637.21 Coefficients: Estimate Std. Error t value Pr(>|t|) (Intercept) -214.656 301.605 -0.712 0.486 head_size 13.654 9.328 1.464 0.160 Residual standard error: 317.9 on 18 degrees of freedom Multiple R-squared: 0.1064, Adjusted R-squared: 0.05673 F-statistic: 2.143 on 1 and 18 DF, p-value: 0.1605 ``` ]] --- class: split-40 count: false .column[.content[ ```r # create artificial data set # set seed for reproducibility set.seed(501) # head_size in cm rnorm(n = 20, mean = 30, sd = 10) -> head_size # tail_length in kilogram the relationship between head_size # and tail_length is completely random head_size * rnorm(20, 0, sd = 15) + 80 -> tail_length # join head_size and tail_length in data frame data.frame(head_size, tail_length) -> df lm(tail_length ~ head_size, data = df) %>% summary() -> *reg ``` ]] .column[.content[ ]] --- beta = ((X'X)^(-1))X'y res = y - beta1 - beta2*X2 VCV = (1/(n-k))res'res(X'X)^(-1) --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector *cbind(1, df$head_size) ``` ]] .column[.content[ ``` [,1] [,2] [1,] 1 35.77281 [2,] 1 36.17452 [3,] 1 34.52007 [4,] 1 32.25781 [5,] 1 21.55195 [6,] 1 15.66631 [7,] 1 13.51793 [8,] 1 30.35623 [9,] 1 31.84019 [10,] 1 42.23762 [11,] 1 30.87002 [12,] 1 39.05107 [13,] 1 32.37906 [14,] 1 34.65357 [15,] 1 39.27268 [16,] 1 28.10562 [17,] 1 28.13692 [18,] 1 40.97114 [19,] 1 24.25709 [20,] 1 36.85942 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% * as.matrix() ``` ]] .column[.content[ ``` [,1] [,2] [1,] 1 35.77281 [2,] 1 36.17452 [3,] 1 34.52007 [4,] 1 32.25781 [5,] 1 21.55195 [6,] 1 15.66631 [7,] 1 13.51793 [8,] 1 30.35623 [9,] 1 31.84019 [10,] 1 42.23762 [11,] 1 30.87002 [12,] 1 39.05107 [13,] 1 32.37906 [14,] 1 34.65357 [15,] 1 39.27268 [16,] 1 28.10562 [17,] 1 28.13692 [18,] 1 40.97114 [19,] 1 24.25709 [20,] 1 36.85942 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> * X ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X *as.matrix(df$tail_length) ``` ]] .column[.content[ ``` [,1] [1,] 697.949367 [2,] 454.088447 [3,] 158.609728 [4,] 300.437392 [5,] -10.055414 [6,] 12.294857 [7,] 292.590425 [8,] -156.913095 [9,] -550.041452 [10,] 262.981543 [11,] 368.245079 [12,] 370.787842 [13,] 347.125890 [14,] 499.402052 [15,] 958.782945 [16,] 298.983754 [17,] -35.725305 [18,] 85.639560 [19,] -63.704121 [20,] -3.675432 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> * y ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta *t(X) %*% X ``` ]] .column[.content[ ``` [,1] [,2] [1,] 20.000 628.452 [2,] 628.452 20909.292 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% *solve() ``` ]] .column[.content[ ``` [,1] [,2] [1,] 0.89994857 -0.0270489556 [2,] -0.02704896 0.0008608121 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% * t(X) ``` ]] .column[.content[ ``` [,1] [,2] [,3] [,4] [,5] [1,] -0.067668557 -0.078534496 -0.033783400 0.0274084332 0.316990793 [2,] 0.003744711 0.004090511 0.002666342 0.0007189591 -0.008496775 [,6] [,7] [,8] [,9] [,10] [,11] [1,] 0.4761911 0.53430277 0.0788442915 0.0387045902 -0.2425350 0.0649468030 [2,] -0.0135632 -0.01541256 -0.0009179473 0.0003594677 0.0093097 -0.0004756704 [,12] [,13] [,14] [,15] [,16] [1,] -0.156341987 0.024128703 -0.037394248 -0.162336382 0.139721007 [2,] 0.006566674 0.000823334 0.002781254 0.006757441 -0.002855302 [,17] [,18] [,19] [,20] [1,] 0.138874346 -0.208278049 0.243819622 -0.097060375 [2,] -0.002828357 0.008219499 -0.006168159 0.004680083 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% * y ``` ]] .column[.content[ ``` [,1] [1,] -214.65587 [2,] 13.65406 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> * beta ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals *y ``` ]] .column[.content[ ``` [,1] [1,] 697.949367 [2,] 454.088447 [3,] 158.609728 [4,] 300.437392 [5,] -10.055414 [6,] 12.294857 [7,] 292.590425 [8,] -156.913095 [9,] -550.041452 [10,] 262.981543 [11,] 368.245079 [12,] 370.787842 [13,] 347.125890 [14,] 499.402052 [15,] 958.782945 [16,] 298.983754 [17,] -35.725305 [18,] 85.639560 [19,] -63.704121 [20,] -3.675432 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - * beta[1] ``` ]] .column[.content[ ``` [,1] [1,] 912.60523 [2,] 668.74431 [3,] 373.26560 [4,] 515.09326 [5,] 204.60045 [6,] 226.95072 [7,] 507.24629 [8,] 57.74277 [9,] -335.38559 [10,] 477.63741 [11,] 582.90095 [12,] 585.44371 [13,] 561.78176 [14,] 714.05792 [15,] 1173.43881 [16,] 513.63962 [17,] 178.93056 [18,] 300.29543 [19,] 150.95175 [20,] 210.98043 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - * (beta[2] * X[,2]) ``` ]] .column[.content[ ``` [,1] [1,] 424.16118 [2,] 174.81524 [3,] -98.07355 [4,] 74.64318 [5,] -89.67117 [6,] 13.04194 [7,] 322.67172 [8,] -356.74297 [9,] -770.13347 [10,] -99.07758 [11,] 161.39988 [12,] 52.23814 [13,] 119.67610 [14,] 240.89605 [15,] 637.20733 [16,] 129.88387 [17,] -205.25257 [18,] -259.12698 [19,] -180.25600 [20,] -292.30033 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% *as.matrix() ``` ]] .column[.content[ ``` [,1] [1,] 424.16118 [2,] 174.81524 [3,] -98.07355 [4,] 74.64318 [5,] -89.67117 [6,] 13.04194 [7,] 322.67172 [8,] -356.74297 [9,] -770.13347 [10,] -99.07758 [11,] 161.39988 [12,] 52.23814 [13,] 119.67610 [14,] 240.89605 [15,] 637.20733 [16,] 129.88387 [17,] -205.25257 [18,] -259.12698 [19,] -180.25600 [20,] -292.30033 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> * res ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters *nrow(df) ``` ]] .column[.content[ ``` [1] 20 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> * n ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n *ncol(X) ``` ]] .column[.content[ ``` [1] 2 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> * k ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV *1/(n - k) ``` ]] .column[.content[ ``` [1] 0.05555556 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * * as.numeric(t(res) %*% res) ``` ]] .column[.content[ ``` [1] 101078.9 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * * solve(t(X) %*% X) ``` ]] .column[.content[ ``` [,1] [,2] [1,] 90965.84 -2734.07953 [2,] -2734.08 87.00997 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * solve(t(X) %*% X) -> *VCV ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * solve(t(X) %*% X) -> VCV ## calculate standard errors se of coefficients *diag(VCV) ``` ]] .column[.content[ ``` [1] 90965.84022 87.00997 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * solve(t(X) %*% X) -> VCV ## calculate standard errors se of coefficients diag(VCV) %>% * sqrt() ``` ]] .column[.content[ ``` [1] 301.605438 9.327913 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * solve(t(X) %*% X) -> VCV ## calculate standard errors se of coefficients diag(VCV) %>% sqrt() -> *se ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * solve(t(X) %*% X) -> VCV ## calculate standard errors se of coefficients diag(VCV) %>% sqrt() -> se ## calculate the p-values *rbind(2*pt(abs(beta[1]/se[1]), df = n - k, * lower.tail = FALSE), * 2*pt(abs(beta[2]/se[2]), df = n - k, * lower.tail = FALSE)) ``` ]] .column[.content[ ``` [,1] [1,] 0.4857664 [2,] 0.1604981 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * solve(t(X) %*% X) -> VCV ## calculate standard errors se of coefficients diag(VCV) %>% sqrt() -> se ## calculate the p-values rbind(2*pt(abs(beta[1]/se[1]), df = n - k, lower.tail = FALSE), 2*pt(abs(beta[2]/se[2]), df = n - k, lower.tail = FALSE)) -> * p_value ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * solve(t(X) %*% X) -> VCV ## calculate standard errors se of coefficients diag(VCV) %>% sqrt() -> se ## calculate the p-values rbind(2*pt(abs(beta[1]/se[1]), df = n - k, lower.tail = FALSE), 2*pt(abs(beta[2]/se[2]), df = n - k, lower.tail = FALSE)) -> p_value ## combine all necessary information *as.data.frame(cbind(c("(Intercept)","head_size"), * beta,se,p_value)) ``` ]] .column[.content[ ``` V1 V2 se V4 1 (Intercept) -214.655866735562 301.605437988381 0.485766378408867 2 head_size 13.6540591513866 9.32791323596427 0.160498082949983 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * solve(t(X) %*% X) -> VCV ## calculate standard errors se of coefficients diag(VCV) %>% sqrt() -> se ## calculate the p-values rbind(2*pt(abs(beta[1]/se[1]), df = n - k, lower.tail = FALSE), 2*pt(abs(beta[2]/se[2]), df = n - k, lower.tail = FALSE)) -> p_value ## combine all necessary information as.data.frame(cbind(c("(Intercept)","head_size"), beta,se,p_value)) -> * output ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * solve(t(X) %*% X) -> VCV ## calculate standard errors se of coefficients diag(VCV) %>% sqrt() -> se ## calculate the p-values rbind(2*pt(abs(beta[1]/se[1]), df = n - k, lower.tail = FALSE), 2*pt(abs(beta[2]/se[2]), df = n - k, lower.tail = FALSE)) -> p_value ## combine all necessary information as.data.frame(cbind(c("(Intercept)","head_size"), beta,se,p_value)) -> output *c("Coefficients:","Estimate", * "Std. Error","Pr(>|t|)") ``` ]] .column[.content[ ``` [1] "Coefficients:" "Estimate" "Std. Error" "Pr(>|t|)" ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * solve(t(X) %*% X) -> VCV ## calculate standard errors se of coefficients diag(VCV) %>% sqrt() -> se ## calculate the p-values rbind(2*pt(abs(beta[1]/se[1]), df = n - k, lower.tail = FALSE), 2*pt(abs(beta[2]/se[2]), df = n - k, lower.tail = FALSE)) -> p_value ## combine all necessary information as.data.frame(cbind(c("(Intercept)","head_size"), beta,se,p_value)) -> output c("Coefficients:","Estimate", "Std. Error","Pr(>|t|)") -> * names(output) ``` ]] .column[.content[ ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * solve(t(X) %*% X) -> VCV ## calculate standard errors se of coefficients diag(VCV) %>% sqrt() -> se ## calculate the p-values rbind(2*pt(abs(beta[1]/se[1]), df = n - k, lower.tail = FALSE), 2*pt(abs(beta[2]/se[2]), df = n - k, lower.tail = FALSE)) -> p_value ## combine all necessary information as.data.frame(cbind(c("(Intercept)","head_size"), beta,se,p_value)) -> output c("Coefficients:","Estimate", "Std. Error","Pr(>|t|)") -> names(output) #compare automatic lm and manual output *output ``` ]] .column[.content[ ``` Coefficients: Estimate Std. Error Pr(>|t|) 1 (Intercept) -214.655866735562 301.605437988381 0.485766378408867 2 head_size 13.6540591513866 9.32791323596427 0.160498082949983 ``` ]] --- class: split-40 count: false .column[.content[ ```r ## build OLS estimator manually # define X matrix and y vector cbind(1, df$head_size) %>% as.matrix() -> X as.matrix(df$tail_length) -> y # estimate the coeficients beta t(X) %*% X %>% solve() %*% t(X) %*% y -> beta ## calculate residuals y - beta[1] - (beta[2] * X[,2]) %>% as.matrix() -> res ## define the number of observations and the number of # parameters nrow(df) -> n ncol(X) -> k ## calculate the Variance-Covariance matrix VCV 1/(n - k) * as.numeric(t(res) %*% res) * solve(t(X) %*% X) -> VCV ## calculate standard errors se of coefficients diag(VCV) %>% sqrt() -> se ## calculate the p-values rbind(2*pt(abs(beta[1]/se[1]), df = n - k, lower.tail = FALSE), 2*pt(abs(beta[2]/se[2]), df = n - k, lower.tail = FALSE)) -> p_value ## combine all necessary information as.data.frame(cbind(c("(Intercept)","head_size"), beta,se,p_value)) -> output c("Coefficients:","Estimate", "Std. Error","Pr(>|t|)") -> names(output) #compare automatic lm and manual output output *summary(reg) ``` ]] .column[.content[ ``` Coefficients: Estimate Std. Error Pr(>|t|) 1 (Intercept) -214.655866735562 301.605437988381 0.485766378408867 2 head_size 13.6540591513866 9.32791323596427 0.160498082949983 ``` ``` Length Class Mode call 3 -none- call terms 3 terms call residuals 20 -none- numeric coefficients 8 -none- numeric aliased 2 -none- logical sigma 1 -none- numeric df 3 -none- numeric r.squared 1 -none- numeric adj.r.squared 1 -none- numeric fstatistic 3 -none- numeric cov.unscaled 4 -none- numeric ``` ]] <style type="text/css"> .remark-code{line-head_size: 1.5; font-size: 80%} </style>